Комплексные экспоненциальные функции

Многие формулы гармонического анализа записываются значительно проще и некоторые задачи решаются легче, если использовать в качестве элементарных функций не обычные действительные синусоиды, а экспоненциальные функции мнимого аргумента. Действительно, по формуле Эйлора:

Этой записи можно дать геометрическую трактовку, пользуясь представлением комплексных чисел в виде точек или векторов на плоскости.

Выражение представляет в данном случае вектор единичной длины, проведенный под углом к действительной оси.

При изменении времени t этот вектор, единичной длины, меняет положение, вращаясь в положительном направлении с угловой скоростью .

Изобразить синусоиду в форме, это значит представить ее суммой двух векторов, длина каждого из которых равна 1/2, расположенных в любой момент времени симметрично относительно действительной оси и вращающихся в разных направлениях с угловыми скоростями .

В момент t=0 они занимают положения под углами относительно действительной оси. Геометрическая сумма векторов всегда совпадает по направлению с действительной осью и представляет действительную функцию времени

При представлении косинусоиды в виде 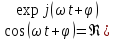 можно ограничиться одним вращающимся в положительном направлении вектором и представить косинусоиду его проекцией на действительную ось. В этом случае нет необходимости вводить отрицательные частоты. Длина вектора представляет амплитуду косинусоиды, а угол, образуемый им в данный момент с действительной осью, - полную фазу 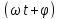. Проекция этого вектора на мнимую ось равна , т.е. представляет ту же косинусоиду, сдвинутую по фазе на .

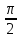Многие сигналы в системах электросвязи можно представлять в виде: 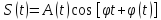, т.е. как «квазигармоническую» функцию с переменными «амплитудой» и «начальной фазой». Такой  сигнал можно интерпретировать геометрически как проекцию на действительную ось вращающегося вектора, но при  этом изменяющего свою длину и угловую скорость.

Рассмотрим отрезок сигнала на некотором интервале времени 0<t<T.

Его можно представить на этом интервале рядом Фурье в экспоненциальной форме:

.

Пользуясь геометрическим представлением синусоиды, можно представить сигнал S(t) в виде суммы вращающихся векторов, каждый из которых имеет вид:

.

Векторы с индексами k>0 вращаются в положительном направлении, а с k<0 в отрицательном. Пара таких векторов с индексами k и –k образует одну действительную косинусоиду.

Поэтому предполагая среднее состояние сигнала нулевым (S0=0), косинусоида может быть представлена проекцией на действительную ось одного вектора, вращающегося в положительном направлении. В результате можно взять действительную часть суммы векторов, вращающихся только в положительном направлении, увеличив их величину вдвое:

.

Ряд в правой части представляет собой комплексную функцию времени, которую обозначим и будем называть комплексным или аналитическим сигналом:

Его геометрическим представлением является вектор, образующийся при суммировании элементарных векторов S_k, k=1,2,… Так как элементарные векторы вращаются с разными угловыми скоростями , то их взаимная конфигурация со временем изменяется. Поэтому их векторная сумма представляет собой вектор с переменной длиной, вращающийся с переменной угловой скоростью.

Исходный сигнал является действительной частью аналитического сигнала.

В результате получим обычное разложение сигнала в ряд Фурье в тригонометрической форме.

Мнимая часть аналитического сигнала представляет собой некоторую функцию времени, однозначно определяемую исходным сигналом S(t).

Ее обозначают 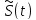и называют сигналом, сопряженным по Гильберту с S(t):

Отсюда видно, что сопряженный сигнал можно получить из исходного, повернув начальные фазы всех его составляющих на –π/2 или, другими словами, заменив в ряде Фурье cos на sin, а sin на –cos.

Аналитический сигнал может быть выражен через реальный и сопряженный сигналы следующим образом:

.

Исходя из этого, аналитический сигнал в момент времени t может быть представлен точкой на комплексной плоскости, если по оси абсцисс откладывать значения реального сигнала S(t), а по оси ординат - сопряженного с ним сигнала .