Системы базисных функций
Один и тот же сигнал может быть разложен по различным СБФ или, что одно и то же, рассмотрен в различных системах координат. При этом внутренние закономерности сигналов не могут нарушаться при изменении системы координат. Однако спектральному анализу в различных СБФ соответствует различная физическая интерпретация и, что особенно важно, различная практическая реализация. Так, например, технические характеристики (точность, быстродействие, затраты памяти и оборудования) цифровых фильтров, построенных в спектральной области, зависят от применяемых СБФ и для различных систем существенно различны. В соответствии с этим, при решении практических задач целесообразно подбирать наиболее подходящие СБФ. Выбор базиса во многом обусловлен спецификой решаемых задач и требованиями, предъявляемыми при их решении.
СБФ существует бесчисленное множество. Краткий обзор некоторых СБФ, применяемых в настоящее время в теории и практике обработки сигналов.
Системы единичных функций. Два прямоугольных импульса, не перекрывающие друг друга, ортогональны. Поэтому система прямоугольных импульсов, приставленных друг к другу и заполняющих интервал [t0, tN], будет ортогональной системой.
Такая
система полна только для подмножества
ступенчатых сигналов с шириной ступени
∆t,
где ∆t
- длительность импульсов, N
= T
/ ∆t
- число импульсов на рассматриваемом
интервале. Система таких функций будет
полна для любого непрерывного сигнала
при ∆t
-> 0 и N
-> ∞. В этом случае она превращается в
систему единичных импульсов {
(t)},
имеющих единичную амплитуду и бесконечно
малую длительность, положение которых
определяется сдвигом по оси a∆t
= t
при ∆t
-> 0, a
-> ∞. Система функций {
(t)}
является полной ортогональной системой.
Из
нее дискретизацией можно получить
систему дискретных единичных функций
{
(i)},
каждая из которых имеет вид единичного
импульса бесконечно малой длительности
и аналитически записывается в виде
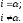
Такая система определена на целочисленном интервале [0, N). Для N=8 она приведена
.
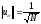Эта система представляет собой полную СБФ, служащую для разложения дискретных сигналов произвольной формы.
-
Системы тригонометрических базисных функций:
Система
тригонометрических функций {cos(kξ)
, sin(kξ)}
= { 1, sin(ξ),
cos(ξ),
sin(2ξ),
cos(2ξ),
...} является полной ортогональной
системой с интервалом ортогональности
[-π,
π],
либо [0, 2π].
Система является периодической с
периодом 2π
и ненормированной (норма равна 1/
).
Проведя нормирование на ее основе, можно
получить полную ортонормированную
систему { 1,
sin(ξ),
cos(ξ),
sin(2ξ),
cos(2ξ),
...}.
Дискретный аналог этой СБФ - полная ортонормированная система дискретных тригонометрический функций
определенная
на интервале [-N/2,
N/2)
или [0, N).
В качестве примера приведена система из восьми функций с интервалом определения [-4, 4).
-
Системы комплексных экспоненциальных функций -
.
Эти функции используются в преобразованиях
Фурье и Лапласа. -
Системы комплексных дискретных экспоненциальных, базисных функций -
.
Эти функции используются в дискретных
преобразованиях Фурье и Лапласа, быстром
преобразовании Фурье. -
Полиномиальные СБФ, использующие полиномы Чебышева и Лежандра. Эти функции часто используются для анализа и синтеза цифровых фильтров.
-
Двоично – ортогональные СБФ Уолша, Хаара, Радемахера. Эти функции широко используются в вычислительной технике для анализа и синтеза цифровых автоматов.
Базисные функции составляют ядро различных интегральных преобразований, используемых для исследования сигналов и систем (Фурье, Лапласа, Карсона, Хэвисайда, Уолша, Хаара и др.), которые имеют следующую структуру записи:
,
.
(5)
При этом, различным СБФ соответствует различная интерпретация сигналов.