11.6. Магнитные волны ( , )

Будем рассуждать аналогично случаю с электрическими волнами

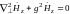
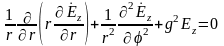
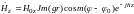
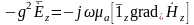
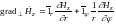
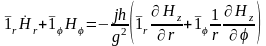
(11.37)

Отметим, что при выполнении J_m(ga)=0 согласно

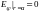
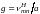(11.38)

Несколько первых корней функции Бесселя в порядке их возрастания и соответствующие длины волн 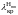представлены в таблице.

Тип волны	H11	H21	H01	H31	H41	H12	H51	H21	H02
	1.84	3.05	3.83	4.20	5.32	5.33	6.42	6.71	7.02
	3.41	2.06	1.64	1.50	1.182	1.178	0.979	0.934	0.838

Низшим типом среди не только волн H, но и всех волн в круглом волноводе, как следует из сравнения двух таблиц, является волна H₁₁.

Рис.11.6.Структура поля волныН₁₁

Рис.11.7.Диаграмма типов волн круглого волновода

11.7 Коаксиальный волновод

Рис. 11.8 Структура поля коаксиального волновода

11.8 Волна t. Волновое сопротивление коаксиальной линии

В коаксиальных линиях возможно существование волн T, E и H.

Так как у волныT , то эта волна является низшим типом волны в коаксиальной линии.

Уравнение Лапласа (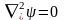 ) в полярной системе координат имеет вид

_(11.39)

Уравнению (11.39) соответствуют два решения:

_(11.40)

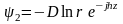, (11.41)

где m - целое число.

На поверхности внутреннего проводника и на внутренней поверхности внешнего проводника, которые полагаются идеально проводящими, касательная составляющая электрического поля должна обращаться в нуль

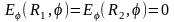(11.42)

Следовательно, решение (11.40) при и не удовлетворяет граничному условию (11.42) и его следует отбросить. Для второго решения

,

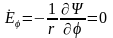т.е. граничное условие (11.42) выполняется тождественно при произвольном значении константы D и функция ₂ является искомым решением.

Подставляя в ( ) функцию ₂, находим

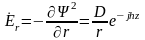, (11.43)

(11.44)

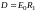, где E₀ - модуль напряженности эле критического поля у поверхности внутреннего проводника.

Структура поля, соответствующая (11.43), (11.44) изображена на рис.11.8

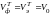
Разность потенциалов между центральным и внешним проводниками равна

(11.45)

Ток, текущий по поверхности центрального проводника и по внутренней поверхности внешнего проводника, равен

(11.46)

Отношение напряжения u к току I в режиме бегущей волны называется волновым сопротивлением коаксиальной линии

(11.47)

11.9 Электрические и магнитные волны

Продольная составляющая E_z волны E является решением уравнения (11.39), которое согласно (11.47) имеет вид

(11.48)

Так как E_z обращается в нуль у поверхности внутреннего и внешнего проводника, то

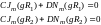
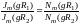(11.49)

(11.49) - трансцендентное уравнение, из которого находится величина. Аналогично в случае магнитных волн: величина является корнем

трансцендентного уравнения:

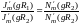(11.50)

Как показывает анализ уравнений (11.49) и (11.50), первым высшим типом волны в коаксиальной линии при любом диаметре внутреннего проводника является волна H₁₁.

Если R₁ = 0, то коаксиальная линия превращается в круглый волновод, низшим типом волны, в котором является волна H₁₁; введение вдоль оси круглого волновода тонкого металлического стержня слабо влияет на распространение волны H₁₁ ввиду отсутствия у нее продольных составляющих E. Поэтому при малом R₁

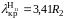(11.51)

Рис.11.9Структура поляН₁₁в линии передач

Рассмотрим другой предельный случай

- структура поля волны H в прямоугольном волноводе, изогнутом в поперечной плоскости по дуге 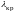у H₁₁ равна размеру широкой стенки прямоугольного волновода, длину которой в изогнутом волноводе можно считать равной . Следовательно, при

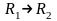
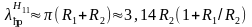(11.52)

При формула (11.52) дает значение 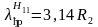, что отличается менее чем на 10% от значения в формуле (11.51)

Таким образом, можно без большой погрешности пользоваться формулой (11.52) при произвольных значениях R₁ и R₂.