11. Направляющие системы

11.1. Прямоугольный волновод.Электрические волны ( и ).

_Рис.11.1 Прямоугольный волновод

_,

_.

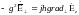имеет в декартовой системе координат вид:

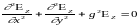, (11.1)

Решение (11.1) . (11.2)

где Х(Х) - функция только Х , Y(y) - функция только Y.

11.2 (11.1) 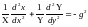 (11.3)

Выполнение (11.3) при произвольных значениях Х и Y возможно, если

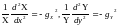, (11.4)

где 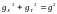,(11.5)

. (11.6)

Решение (11.6) имеет вид:

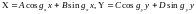(11.7)

11.7 (11.2) 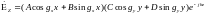 (11.8).

Так как стенки волновода предполагаются идеально проводящими, то, применяя граничное условие : при х=0, х=a и при y=0, y=b

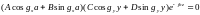
это возможно, если:

для этого необходимо : (11.9)

где 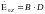и имеет смысл амплитуды продольной составляющей .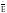

11.1и (11.2) в декартовой системе координат имеют вид:

Подставляя (11.9) получим:

(11.10)

Как следует из (11.9), (11.10) структура поля волн типа Е в плоскости поперечного сечения соответствуют структуре стоячих волн, причем m равно числу полуволн, укладывающихся вдоль стенки длиной а, и n - число полуволн, укладывающихся вдоль стенки длиной b. Каждой паре чисел m и n соответствует определенная структура ЭМП, обозначаемая Е_mn.

Отметим, что структуру волны Е_z1 можно получить повторением структуры волны Е₁₁ вдоль соответствующей координаты.

,

,

,

.

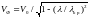
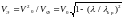Низшим типом среди волн Е_mn , обладающей наибольшей _кр, является волна Е₁₁. Волны Е_mn с различной структурой поля, которым соответствуют одинаковые значения g, имеющие равные коэффициенты распространения, фазовые скорости и скорости распространения энергии, называются вырожденными.

11.2. Магнитные волны ( и ).

,

.

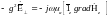имеет в декартовой системе координат вид:

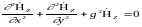, (11.11)

. (11.12)

На поверхности идеально проводящих стенок волновода должно выполнятся граничное условие: .

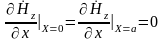, (11.12)

. (11.13)

Подставляя (11.13), (11.14) в (11.12), приходим к соотношениям

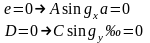(11.15)

Как следует из (11.15), у волн Н, как и у волн Е,

,

т.е. волны Н и Е с равными индексами являются вырожденными.

Подставляя в (11.12) (11.15) и значения 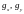, получим:

.(11.16)

где Н0Z- =АС - амплитуда продольной составляющей магнитного поля.

Соотношения (11.1) , (11.2) в декартовой системе координат имеет вид:

(11.17)

Как следует из равенств (11.16), (11.17), у волн Н, в отличие от волн Е, обращение в нуль одного из индексов (m или n) не влечет за собой обращения в нуль всех составляющих поля. Поэтому, если полагать аb, то низшим типом волн Н является волна Н₁₀.

,

Поскольку 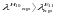, то волна Н₁₀ является низшим типом волны не только среди волн Н, но и среди всех возможных типов волн в прямоугольном волноводе. Это означает, что при а передача энергии по прямоугольному волноводу невозможна. ,

,

.