Условия баланса:

Ė₁· + Ė₂· = _ист = _нагр

и - сопряженные комплексы токов, т.е.

Если İ= I· , то = I· или

İ=I_a + jI_p ; то = I_a -jI_p

_ист = _ист1+ _ист2 = 100e ^{j 0°}·7,972e ^{–j 61,31°}+120e ^–j45˚·13,286e ^j103,64˚=797,2e^{–j 61,31º} +1594,32e ^{j 58,64º} = 382,71 –j 699,33+829,7+j 1361,41=1212,41+j 662,08=

=1381,41e ^{j 28,64º} BA

Мощности источников по расчёту:

Полная S_ист =1381,41 BA

Активная Р_ист = 1212,41 Вт

Реактивная Q_ист = 662,08 BAр

Т.к реактивная мощность положительная (со знаком +) ,

то из этого следует, что в цепи преобладает реактивная индуктивная нагрузка, т.е. характер нагрузка активно-индуктивный.

Мощности нагрузок ветвей:

= ·Z₁=7,972² ·8,846·e ^{– j47,29˚}=526,19e ^{–j 47,29º}=381,32 –j 413,1 BA

= ·Z₂=13,286² ·6,466·e ^j51,78˚= 1141,36e ^j51,78º=706,14+j896,7 BA

= ·Z₃= 5,958² ·6,07e ^j54,79º= 215,47e ^j54,79º= 124,24+j176,05 BA

= + + , но при этом надо знать, что модуль суммарной полной мощности не равен сумме модулей нагрузок (S≠S1+S2+S3) , т.к. коэффициенты мощности нагрузок разные ; т.е. нельзя складывать модули мощностей нагрузок . Необходимо суммировать алгебраические выражения мощностей нагрузок.

= + + = 381,32+706,14+124,24 -j 413,1+j896,7 +j176,05 = 1211,7+ j· ·659,74=1379,66e ^{j 28,57º}≈1381,41e ^{j 28,64º}

=1379,66e ^{j 28,57º} ВА (разница 1,75Вт или 0,127%)

P_нагр =1211,7 Вт (разница 0,75Вт или 0,058%)

Q_напр=659,74 BAр (разница 2,34Вт или 0,354%)

Разница объясняется неточностями при расчетах в результате округления тысячных долей и намного меньше допустимых при электрических расчетах 5%.

5. 0пределим показания ваттметра. Показания ваттметра определяются условиями его подключения в цепь: приложенным напряжением, протекающим по токовой обмотке прибора током и углом сдвига фаз между током и напряжением ваттметра.

В общем случае P_w=Re( · ), т.е

Активная мощность определяется как реальная (Rе) часть этого выражения. Если измеряемый ток входит в начало токовой обмотки ваттметра, обозначенной на схеме и приборе значком * , то в этом выражении ток необходимо брать с «плюсом», если наоборот, то со знаком «минус».

По закону Ома:

=Ė₁ –İ₁·R₁, а из расчета İ_w=İ₁, тогда P_w= Re[(Ė₁-İ·R₁)· ] Вт, т.к. измеряемый ток входит в начало токовой обмотки, обозначенной знаком *.

=Ė₁ –İ₁·R₁= 100e ^{j 0º} -7,972e ^{j 61,31º}·6 =100e ^{j 0º} -47,832e ^j61,31º= 100-(22,963+j 41,96)= =77,037 –j 41,96 =87,723e ^{–j 28,58º} B

P_w= Re[87,723e ^{–j 28,58º}·7,972e ^{- j 61,31º}]= 699,33e ^{–j 89,89º}= Re 699,33e ^{–j 89,89º}= 1,34 Вт, т.е. практически ваттметр покажет нулевое значение.

6. Вычислим напряжения на всех элементах цепи.

В общем случае падение напряжения на каждом элементе цепи определяется по закону Ома:

=İ·R ; =İ·X_L; =İ·X_C; где İ- ток протекающий через соответствующий элемент цепи.

= =İ₁·R₁=7,972e ^{j 61,31º}·6=47,832e^{j 61,31º}=22,963+j 41,96 B

= = İ₁·X_C1=7,972e ^{j 61,31º}·15,92e ^{–j 90º}=126,91e ^{–j 28,69º}=111,33 –j 60,92 B

= =İ₁· X_L1= 7,972e ^{j 61,31º}·9,42e^{j 90º}=75,1e^{j 151,31º}= -65,88+j 36,05 B

= = İ₂·R₂= 13,286e ^{–j 103,64º}·4=53,14e ^{–j 103,64º}= -12,53 –j 51,64 B

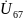= = İ₂·X_C2=13,286e ^{–j 103,64º}·10,62e ^{–j 90º}=141,1e ^{–j 193,64º}= -137,12+j 33,27 B

= = İ₂· X_L2= 13,286e ^{–j 103,64º}·15,7 e ^{–j 90º}=208,59e ^{–j 13,64º}=202,71 –j 49,19 B

= = İ₃· X_L3=5,958e ^{–j 83,32º}·6,28 e^{j 90º} =37,42,e^{j 6,68º}=37,16+j4,35 B

= = =İ₃·(R₃· X_C3)/( R₃+X_C3)=5,958e^{–j 83,32º}·3,74e^{–j 20,64º}=22,28e^{–j 103,96º} =

-5,37- –j 21,62 B

= -Ė₁=100e^{j 0º} B

= Ė₂=120e ^{–j 45º} B

7. Построение векторной топографической диаграммы напряжений и векторной диаграммы токов. Один из вариантов правил построения векторной топографической диаграммы напряжений и векторной диаграммы токов описан в РГР-2, поэтому повторяться не будем. Обозначим точки сопряжений элементов на схеме цепи цифрами от 0 до 8 и выберем направление обхода 1-го контура по направлению 0 -1-2-3-4-5-0,а 2-го -по направлению 0-1-2-6-7-8-0. В этом случае потенциал очередной точки повышается по сравнению с предыдущим повышается на величину напряжения на этом элементе цепи. Так, если φ₀=0, то

φ₁=φ₀+İ₃· Z_C3R3; φ₂=φ₁+ İ₃· X_L3 и т.д. или

φ₁=φ₀+ = φ₀+ ; φ₂=φ₁+ и т.д. ; где Z_C3R3=

Для удобства и для большей точности в масштабе по оси абсцисс (вещественной от ± 1) откладываем активные (вещественные) составляющие напряжений, а по оси ординат (мнимой оси ±j ) реактивные (мнимые) составляющие.

Аналогично строим и векторную диаграмму токов на которой проверим правильность расчетов, сложив графически соответствующие вектора.

İ₃=İ₁+İ₂ ; İ₃= İ'₃+İ''₃ (см. РГР-2)

2-я задача:

Расчет при наличии индуктивной связи между катушками. Исходные данные те же, что и в предыдущей задаче, дополнительно заданы коэффициенты магнитной связи между катушками.

К₁₂=0,6; Ki3=O,7 ;К₃₂=0,8