Лекция 1. Алгебра (2 час)
Рассматриваемые вопросы: Решение балансовых условий в экономике, инженерии и других отраслях с помощью систем линейных алгебраических уравнений. Матрица. Элементы, размерность матрицы. Операции с матрицами. Определители 2-го и 3-го порядка. Метод Крамера для системы линейных алгебраических уравнений с 3-я неизвестными. Основные понятия для векторов: вектор; длина вектора; геометрическая сумма векторов; умножение вектора на число; скалярное произведение векторов. Теоремы: разложение вектора на составляющие; длина вектора; арифметическая сумма векторов; умножение вектора на число; вектор, проходящий через 2 точки. Векторное произведение векторов. Площадь треугольника. Смешанное произведение векторов. Объем пирамиды и параллелепипеда. Уравнения прямых. Свойства прямых.
Содержание лекции
Введение 2
1. Матричный анализ 3
2. Метод Крамера 5
3. Векторный анализ 7
4. Аналитическая геометрия 11
Литература 13
Введение
В экономике, инженерии и других отраслях большую роль играет матричный и векторный анализ. В таблицах, т.е. матрицах, отражается основная экономическая и инженерная информация. С помощью систем линейных алгебраических уравнений решаются условия баланса в экономике и инженерии. Векторный анализ применяется во всех тех случаях, где важны не только значения величин, но и их направленность. Например, слова «вектор развития региона» означают, что развитие региона может производиться по указанным направлениям развития.
Рассмотрим пример применения матричного анализа в экономике.
Американский экономист российского происхождения Леонтьев Василий Васильевич (1905-1995), лауреат Нобелевской премии по экономике в 1973 г., автор теории японского экономического чуда, разработал межотраслевой баланс и модели его расчета
Пусть
– конечный выпуск (для конечного
потребления) продукции
-й
отрасли,
,
а
–
вектор конечного выпуска (для конечного
потребления) всех отраслей. Обозначим
– матрица технологических коэффициентов,
где элементы матрицы
– необходимый объем продукции
-й
отрасли для производства единицы
продукции
-й
отрасли. Пусть также
– совокупный выпуск
-й
отрасли, соответственно,
– вектор совокупного выпуска всех
отраслей.
Совокупный
выпуск всех отраслей
складывается
из двух компонент: выпуска для конечного
потребления
и выпуска для межотраслевого потребления
(для обеспечения производства продукции
других отраслей). Выпуск для межотраслевого
потребления с помощью матрицы
технологических коэффициентов
определяется как
.
Соответственно в сумме с конечным
потреблением
получим
совокупный выпуск
:
X = AX + Y.
Откуда
X – AX = Y;
(E – A) X = Y; X = (E – A)-1 Y,
где
E
– это единичная матрица, диагональные
значения которой равны единице, а
остальные равны нулю,
– представляет собой обратную матрицу.
Математическое решение этой задачи
можно записать в следующем виде для
достаточно большого числа
:
,
.
1. Матричный анализ
Определение.
Матрицей
размерности
называется таблица, содержащая
строк и
столбцов:
,
где
– элемент матрицы,
– номер строки, где стоит элемент
,
,
– номер столбца, где стоит элемент
,
.
Пример.
Матрица
имеет размерность
:
,
матрица
имеет размерность
:
,
Матрица
имеет размерность
(квадратная матрица)
.
▲
Матрицы одинаковой размерности можно складывать и вычитать, матрицы можно умножать на числа, а также матрицы соответствующей размерности можно перемножать между собой. Рассмотрим операции с матрицами на примерах.
Пример. Сумма матриц
;
вычитание матриц
;
произведение матрицы на число
.
▲
Определение.
Произведением матрицы
размерности
на матрицу
размерности
называется матрица
размерности
,
такая, что ее элементы вычисляется по
правилу:
-я
строка матрицы
умножить
скалярно
-й
столбец матрицы
.
Пример.
.
▲
В
примере отдельным типом линии выделены
для каждого скалярного произведения:
строка матрицы
,
столбец матрицы
,
строка в произведении
.
Определение.
Для каждой
квадратной матрицы размерности
однозначно
определяется число
,
называемое определителем
-го
порядка.
Определение. Определитель 2-го порядка вычисляется по правилу крестов
.
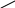Пример.
.
▲
Определение. Определитель 3-го порядка вычисляется по правилу крестов + –
,
где справа показана сумма произведений элементов определителя со знаком плюс или минус. Произведения элементов берутся вдоль указанных ломанных. Произведения со знаком плюс показаны знаком +, произведения со знаком минус показаны знаком –.
Пример.
.
▲
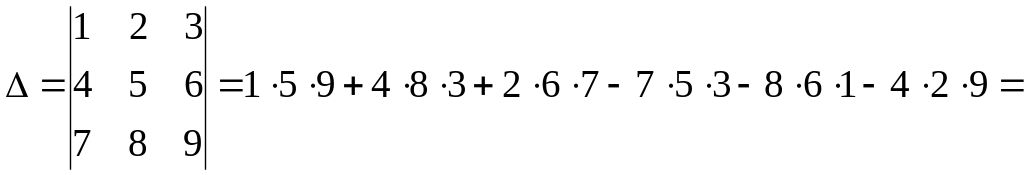