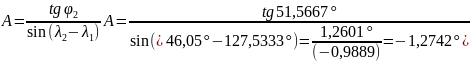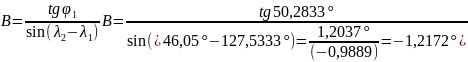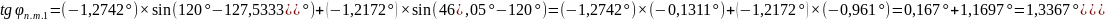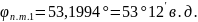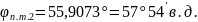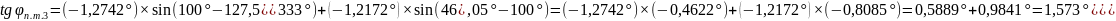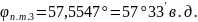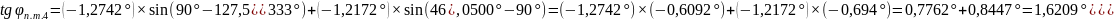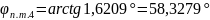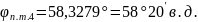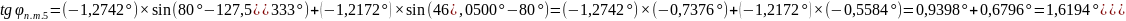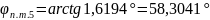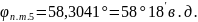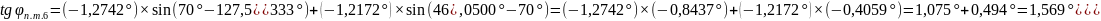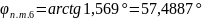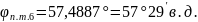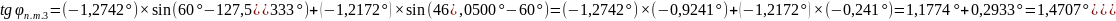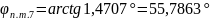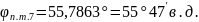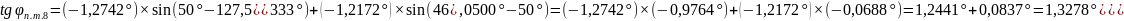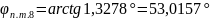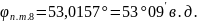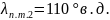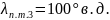ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА)

Кафедра управления воздушным движением

КУРСОВАЯ РАБОТА

«Расчет навигационных элементов полета»

по дисциплине

«Воздушная навигация»

Выполнил:

Студент группы УВД 2 – 1

Андрей

Руководитель:

доцент кафедры УВД

Чехов И.А.

__________________________

(дата, подпись)

Курсовая работа защищена

с оценкой

__________________________

Москва – 2017

Оглавление

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ 1

Введение 3

1. Вычисление длины пути ортодромии 4

2. Вычисление заданного путевого угла и длины пути локсодромии 9

3. Расчет элементов маршрута захода на посадку 14

Заключение 21

Приложение 22

Используемая литература 23

Введение

Целью данной курсовой работы является определение навигационных элементов полета, таких как ортодромия, локсодромия и заход на посадку с прямой. Определение всех этих навигационных элементов очень важны в авиации.

Аэронавигация – прикладная наука о точном, надежном и безопасном вождении воздушного судна из одной точки в другую, о методах применения технических средств навигации.

Целью полета гражданского ВС является:

1. перевозок пассажиров, багажа, груза и почты;

2. выполнения авиационных работ в отдельных отраслях народного хозяйства (в сельском хозяйстве, строительстве, для охраны лесов, обслуживания экспедиций и т.п.);

3. оказания медицинской помощи населению и проведения санитарных мероприятий;

4. проведения экспериментальных и научно-исследовательских работ;

5. проведения учебных, культурно-просветительных и спортивных мероприятий;

6. проведения поисково-спасательных, аварийно-спасательных работ и оказания помощи при стихийных бедствиях.

При осуществлении этих целей к аэронавигации, как правило, предъявляются определенные требования такие, как безопасность, точность, экономичность, регулярность.

Аэронавигации включает в себя решение трех основных задач:

- формирование (выбор) заданной траектории;

- определение местоположения ВС в пространстве и параметров его движения;

- формирование навигационного решения (управляющих воздействий для вывода ВС на заданную траекторию).

1. Вычисление длины пути ортодромии

Ортодромией в навигации называется дуга большого круга на земной сфере. Большой круг – это линия, образованная сечением сферы плоскостью, проходящей через центр сферы. Таким образом, термин ортодромия применим только к линии на сфере.

Рис.1 Ортодромия

Значение ортодромии для навигации обусловлено тем, что она является линией, соединяющей две точки по кратчайшему расстоянию по поверхности между двумя точками (рис.1).

Отрезком ортодромии является линия заданного пути (ЛЗП) участка маршрута между двумя ППМ. Ортодромией является и линия равных пеленгов самолета (ЛРПС), используемая для определения места ВС [5].

Свойства ортодромии:

1. Ортодромия является кратчайшим расстоянием;

2. Ортодромия пересекает меридиан под различными углами. Из этого следуют, что лететь по ортодромии можно только с использованием специальных курсовых приборов;

3. Ортодромия выпуклустью обращена к полюсу. Ближайшая к полюсу точка называется вертиксом. В точках вертекса ортодромия пересекает меридиан под прямым углом, т.е. путевой угол ортодромии составляет 90° (или 270°, если лететь по этой же ортодромии в противоположную сторону). В точках вертекса ортодромия ближе всего подходит к полюсам.

Любая ортодромия имеет две точки вертекса (кроме экватора, на котором все точки имеют одинаковую нулевую широту). Точки вертекса расположены симметрично на противоположных концах диаметра ортодромии (он же диаметр сферы). Поэтому их широты отличаются только знаком, а долготы различаются на 180°.

Математический расчет ортодромии дает хорошую точность, но связан с громоздкими вычислениями. Поэтому иногда ортодромию наносят на полетную карту при помощи навигационного глобуса или сетки, составленной в центральной полярной проекции, на которой ортодромия для любых расстояний изображается прямой линией. Используя это свойство сетки, можно произвести графический расчет ортодромии. Для этого на сетке соединяют начальную и конечную точки ортодромии прямой линией. На этой прямой намечают промежуточные точки. Затем по координатам переносят их на полетную карту и через полученные на полетной карте точки проводят ортодромию [1].

Полет из одной точки в другую по магнитному компасу удобно выполнять с постоянным путевым углом, т.е. по локсодромии.

Расчет длины пути ортодромии вычисляется по следующей формуле:

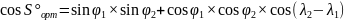
где S_орт — длина пути по ортодромии в градусах дуги; φ₁ и λ₁— координаты исходной точки ортодромии; φ₂ и λ₂ — координа­ты конечной точки ортодромии.

Для перевода S из угловой меры в линейную можно поступить одним из двух способов. Если S выражена в градусах, перевести в угловые минуты (с учетом того, что градус содержит 60′). и умножить на среднюю длину одной минуты (1,853 км). Если S выражена в радианах, можно просто умножить на радиус земной сферы.

Ортодромия пересекает меридианы в каждой своей точке под разными углами, называемыми путевыми углами ортодромии.

Путевые углы в навигации принято отсчитывать от северного направления меридиана по часовой стрелке.

Во многих случаях для решения навигационных задач достаточно только рассчитать путевой угол и длину ортодромии. Но часто ортодромию необходимо нанести на карту, чтобы узнать, через какие районы и пункты она проходит. Ортодромия на полетных картах масштаба 1 : 500 000, 1 : 1 000 000 и 1 : 2 000 000 на расстояниях 1000 – 1200 км практически изображается прямой линией.

Экватор и меридианы являют собой частные случаи ортодромии и изображаются на полетных картах прямой линией.

Во всех проекциях (за исключением центральной азимутальной) ортодромия на карте не изображается в виде прямой линии. Правда, аэронавигационные карты специально издаются в таких проекциях, что ортодромия небольшой длины (до нескольких сотен километров) выглядит в виде почти прямой и на практике ее можно прокладывать по линейке. Отклонение будет незаметным и не превысит, например, толщины карандашной линии. Но ортодромию большой протяженности нельзя изображать в виде прямой линии. Кроме того, маршрут большой длины может не уместиться на одном листе карты и ортодромию придется прокладывать по частям.

При необходимости построения ортодромии на карте рассчитывают по формулам координаты промежуточных точек ортодромии и наносят их на карту. Если точки выбраны на небольшом расстоянии друг от друга, каждый участок ортодромии между ними наносят в виде прямой.

Промежуточные точки оротодромии можно рассчитать по следуюшей формуле:

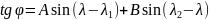, где

,

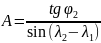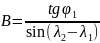
Коэффициенты А,В для всех промежуточных точек остается постоянным.

Задание 1.

Дано:

Аэропорт взлёта: Аэропорт посадки:

Благовещенск Саратов

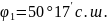
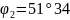’с. ш.

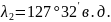
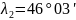в.д.

Найти:

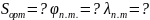
Решение:

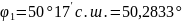
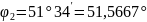
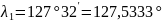
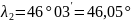
1.

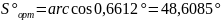
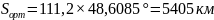
2.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8.