
- •Вычислительная математика. Численные методы. Этапы решения задач.
- •Основы теории погрешностей. Абсолютная и относительная погрешности. Связь между относительной погрешностью и числом значащих цифр.
- •Абсолютная и относительная погрешности.
- •Десятичная запись приближенных чисел. Значащая цифра. Число верных знаков.
- •Округление чисел. Правило и примеры.
- •5. Абсолютные и относительные погрешности суммы, разности, произведения и частного.
- •6.. Метод половинного деления
- •Оценка погрешности метода половинного деления.
- •7. Метод хорд.
- •Оценка погрешностей приближений.
- •8. Приближенное решение нелинейных уравнений. Метод касательных.
- •Оценка погрешностей приближений
- •8. Приближенное решение нелинейных уравнений. Комбинированный метод.
- •10.Приближенное решение нелинейных уравнений. Метод итерации .Достаточное условие сходимости.
- •10.Приближенное решение нелинейных уравнений .Метод итерации. Оценка погрешности метода итерации.
- •11.Численное решение слу. Постановка задачи.Метод Гаусса,ф-лы Крамера.
- •12.Приближ.Реш. Слу. Постановка задачи. Метод итерации. Дост.Усл.Сходимости
- •13.Приближ.Реш. Слу. Постановка задачи. Метод итерации. Оценка погрешности.
- •14.Приближенное решение слу. Постановка задачи. Метод Зейделя. Оценка погрешности приближения.
- •15. Интерполирование функций. Формулы ньютона.
- •16. Интерполирование функций. Формулы лагранжа.
- •17. Приближенное интегрирование функции. Квадратурные формулы Ньютона-Котеса.
- •Квадратурные формулы Ньютона-Котеса
- •18. Приближенное интегрирование функции. Формулы левых и правых прямоугольников. Оценка погрешностей.
- •19. Формула трапеции и ее остаточный член
- •20. Приближенное интегрирование функций. Формула Симпсона и ее остаточный член.
- •20. Приближенное интегрирование функций. Оценка погрешности квадратурных формул (метод пересчета).
6.. Метод половинного деления
Пусть уравнение
 имеет на отрезке
имеет на отрезке
 единственный
корень, причем функция
F(x)
на этом отрезке непрерывна. Разделим
отрезок
пополам точкой
единственный
корень, причем функция
F(x)
на этом отрезке непрерывна. Разделим
отрезок
пополам точкой
 .
Если
.
Если
 (что практически наиболее вероятно), то
возможны два случая:
F(x)
меняет
знак либо на отрезке
(что практически наиболее вероятно), то
возможны два случая:
F(x)
меняет
знак либо на отрезке
 (рис. а),
либо на отрезке [с; b]
(рис. а),
либо на отрезке [с; b]
(рис. б). Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

а
- функция
 меняет
знак на отрезке
;
б - функция
меняет
знак на отрезке
меняет
знак на отрезке
;
б - функция
меняет
знак на отрезке
 .
.
Оценка погрешности метода половинного деления.
Если на каком-то
этапе процесса получен отрезок [a;
b],
содержащий корень, то, приняв приближенно
 ,
получим ошибку, не превышающую значения
,
получим ошибку, не превышающую значения

При
алгоритмизации метода половинного
деления остановить процедуру уточнения
корня можно и другим способом. Зная
допустимое значение погрешности
 :
:

легко
вычислить количество шагов
 получения
последовательных приближений:
получения
последовательных приближений:

Учитывая, что N — число целое, окончательно получим

где, как это принято, квадратные скобки означают целую часть числа.
7. Метод хорд.
Метод
хорд уточнения корней уравнений относятся
к
методам последовательных приближений.
Приближения к корню находятся так: если
известно предыдущее приближение
 ,
то последующее приближение
,
то последующее приближение
 ,
вычисляется по формуле
,
вычисляется по формуле

где Р — некоторое выражение, устанавливающее связь между предыдущим и последующим приближениями. Начинается процесс с какого-либо числа х0 из отрезка изоляции корня — начального приближения.
Итак,
пусть дано уравнение:
 ,
корень
t
которого отделен на отрезке
,
корень
t
которого отделен на отрезке

Известно,
что при
 на
функция возрастает на этом отрезке; при
на
функция возрастает на этом отрезке; при
 — убывает;
при
— убывает;
при
 график функции вогнутый, а при
график функции вогнутый, а при
 -выпуклый. Возможны четыре случая:
-выпуклый. Возможны четыре случая:
 —
функция
возрастает, график вогнутый;
—
функция
возрастает, график вогнутый;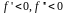 —
функция
убывает, график выпуклый;
—
функция
убывает, график выпуклый; —
функция
возрастает, график выпуклый;
—
функция
возрастает, график выпуклый; —
функция
убывает, график вогнутый.
—
функция
убывает, график вогнутый.
Предположим, что производные
 и
и
 положительны на
положительны на
 (случай 1). Тогда
(случай 1). Тогда
 .
Построим итерационную последовательность,
взяв
.
Построим итерационную последовательность,
взяв
 =а.
Соединим точки
=а.
Соединим точки
 и
и
 отрезком
(хордой).
отрезком
(хордой).
Абсциссу
точки пересечения хорды
 с осью
Ох
возьмем в качестве
с осью
Ох
возьмем в качестве
 .
Уравнение хорды:
.
Уравнение хорды:
 .
.
Положив
в этом уравнении
 ,
получим
,
получим
 .
Следовательно,
.
Следовательно,
 .
.
Далее
напишем уравнение хорды, при
получим
 (абсциссу
точки пересечения хорды
(абсциссу
точки пересечения хорды
 с осью
с осью
 ):
):

Продолжая подобным образом, получим итерационную последовательность, вычисляемую по рекуррентной формуле, где в качестве выбран левый конец а отрезка , а правый конец b этого отрезка остается неподвижным:

Как
видно из схем для случаев
1) и 2)
 ,
неподвижной точкой будет
,
неподвижной точкой будет
 ,
а для
случаев 3) и 4) наоборот,
,
а для
случаев 3) и 4) наоборот,
 ,
неподвижной точкой будет
,
неподвижной точкой будет
 .
.




Правило выбора начального приближения:
Если
 на
(случаи 1-2), то
,
иначе если
на
(случаи 1-2), то
,
иначе если
 (случаи 3-4), то
,
а левый конец а
этого отрезка остается неподвижным.
Для случаев 3)-4) приближения вычисляют
по формуле:
(случаи 3-4), то
,
а левый конец а
этого отрезка остается неподвижным.
Для случаев 3)-4) приближения вычисляют
по формуле:

