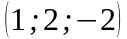- •1.Порядок выполнения, проверки и защиты контрольной работы
- •2.Контрольная работа
- •1.Элементы линейной, векторной алгебры и аналитической геометрии
- •2. Предел и производная функции одной переменной. Исследование функции одной переменной с помощью производной.
- •3. Неопределенный и определенный интегралы. Приложение определенного интеграла.
- •3.Методические рекомендации к выполнению контрольной работы. Решение типового варианта.
- •1.Элементы линейной, векторной алгебры и аналитической геометрии
- •1.1 Элементы линейной алгебры
- •Методы решения систем линейных алгебраических уравнений а) Метод Крамера решения линейной системы
- •Б) Метод последовательного исключения неизвестных (метод Гаусса)
- •1.2 Элементы векторной алгебры
- •1.3. Элементы аналитической геометрии.
- •3. Неопределенный и определенный интеграл и его приложения
- •1. Замена переменных в неопределенном интеграле
- •Определенный интеграл и его приложения
- •4.Титульный лист к контрольной работе.
3.Методические рекомендации к выполнению контрольной работы. Решение типового варианта.
1.Элементы линейной, векторной алгебры и аналитической геометрии
1.1 Элементы линейной алгебры
Пример1.
Даны матрицы
 ,
числа
и
.
,
числа
и
.
Вычислить:
1)
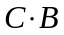 ;
2)
;
2)
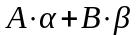 ;
3)
;
3)
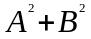 ;
4)
,
если
;
4)
,
если
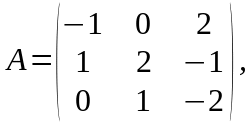
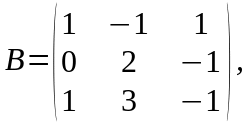
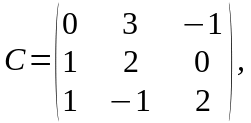
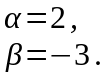
Решение.
1) Убеждаемся в том, что произведение
матриц
и
определено. Действительно, так как
указанные матрицы квадратные одного
порядка, то произведение
и
 существует. Найдем это произведение:
существует. Найдем это произведение:
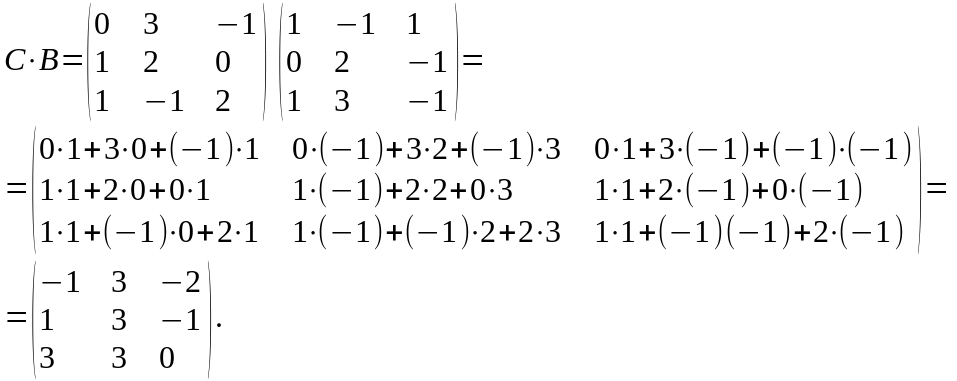
2)
Вычислим линейную комбинацию матриц
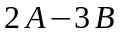 .
Воспользуемся правилом умножения
матрицы на число и правилом вычитания
матриц:
.
Воспользуемся правилом умножения
матрицы на число и правилом вычитания
матриц:
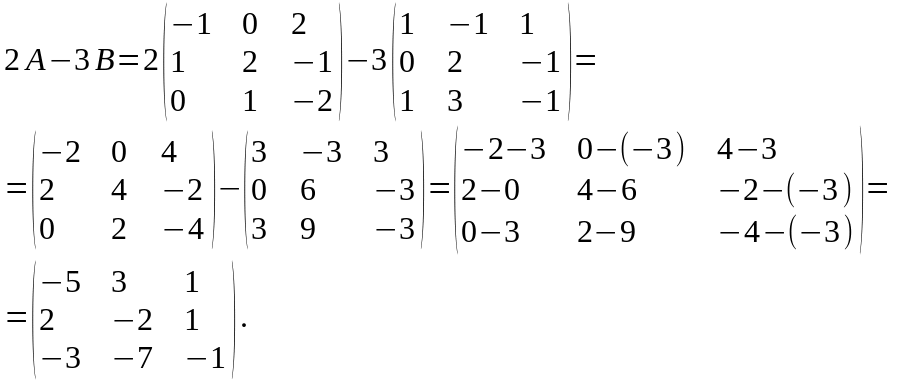
3) Найдем матрицу выражения . Для этого определим матрицу каждого слагаемого, используя определение степени матрицы:
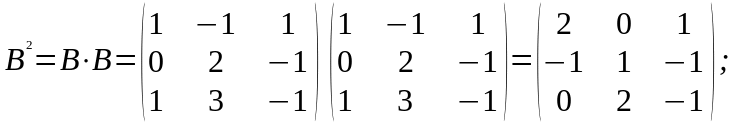
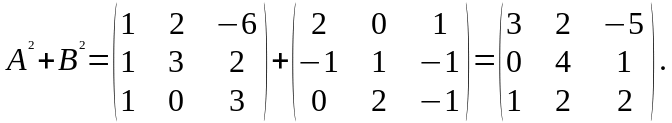
4) Убеждаемся в том, что для матрицы существует обратная матрица. Для этого вычислим определитель
 .
.
Обратная
матрица
существует, так как
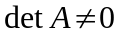 .
Её находим методом присоединенной
матрицы. Для этого определяем алгебраические
дополнения соответствующих элементов
матрицы:
.
Её находим методом присоединенной
матрицы. Для этого определяем алгебраические
дополнения соответствующих элементов
матрицы:
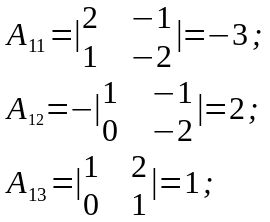
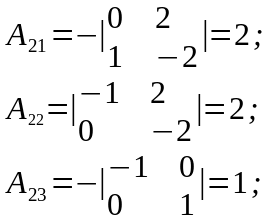
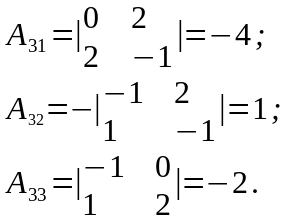
Матрица
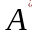 ,
присоединенная к матрице
,
имеет вид
,
присоединенная к матрице
,
имеет вид
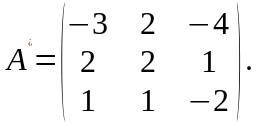
Обратную
матрицу находим по формуле
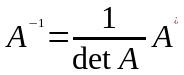 ,
согласно которой
,
согласно которой

Убеждаемся
в правильности нахождения обратной
матрицы. Для этого проверяем равенство
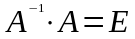 .
Действительно,
.
Действительно,
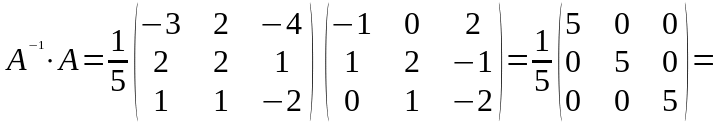
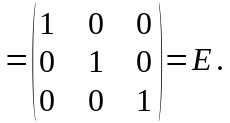
Методы решения систем линейных алгебраических уравнений а) Метод Крамера решения линейной системы
 Если
для линейной системы
Если
для линейной системы
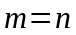 и
,
то верны формулы Крамера для вычисления
неизвестных
и
,
то верны формулы Крамера для вычисления
неизвестных
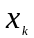
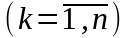 :
:
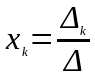 ,
,
где
 ,
а
,
а
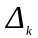 являются
определителями
являются
определителями
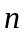 -го
порядка, которые получаются из
-го
порядка, которые получаются из
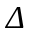 путем замены в нем
путем замены в нем
 -го
столбца столбцом свободных членов
исходной системы.
-го
столбца столбцом свободных членов
исходной системы.
Пример.
Решить систему методом Крамера.
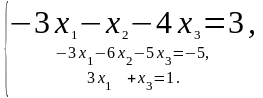
Определитель
системы:
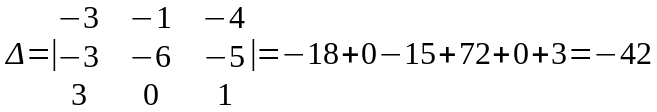 .
.
Последовательно заменив в первый, второй и третий столбцы столбцом свободных членов, получим:
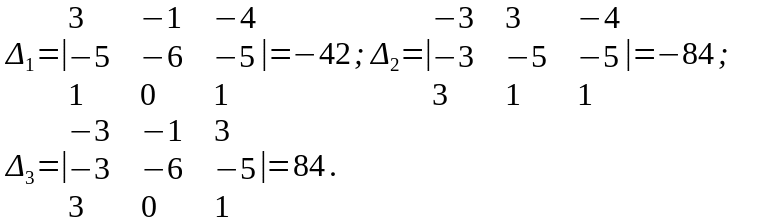
Согласно формулам Крамера, получим решение системы:

Б) Метод последовательного исключения неизвестных (метод Гаусса)
Этот метод является одним из наиболее распространенных методов решения систем линейных алгебраических уравнений. Он основан на элементарных преобразованиях системы уравнений, в результате которых получается более простая для разрешимости система, равносильная исходной системе.
Под элементарными преобразованиями системы линейных уравнений понимаются следующие операции:
умножение какого-либо уравнения системы на число, отличное от нуля;
прибавление к одному уравнению другого уравнения, умноженного на произвольное число;
перемена местами двух уравнений в системе.
Если после указанных преобразований в системе появится уравнение, все коэффициенты которого и свободный член равны нулю, то оно может быть отброшено, поскольку такому уравнению удовлетворяют любые значения неизвестных. В этом случае мы получим систему, равносильную данной и содержащую на одно уравнение меньше, чем данная система.
Если в результате применения элементарных преобразований в системе появится уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, то это указывает на то, что уравнение не удовлетворяется никакими значениями неизвестных, и поэтому полученная система уравнений, равно как и эквивалентная ей исходная система, будет несовместимой.
Если же в процессе преобразования системы этого уравнения не встретим, то система будет совместной. При этом система будет определенной, имеющей единственное решение, если она приведена к треугольному виду (число уравнений равно числу неизвестных) и неопределенной, имеющей бесчисленное множество решений, – если к трапецеидальному виду (число уравнений меньше числа неизвестных). Пример. Решить систему методом Гаусса.
Запишем расширенную матрицу и выполним над ней элементарные преобразования по схеме Гаусса:
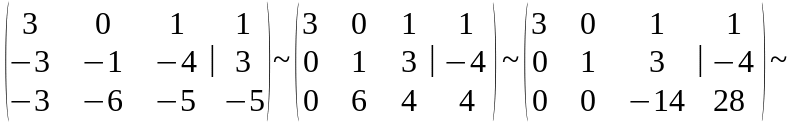
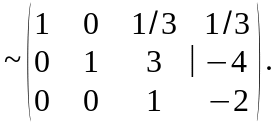
Мы последовательно произвели следующие преобразования:
ко второй и третьей строке прибавили первую строку;
из третьей строки вычли вторую строку, умноженную на шесть;
разделили третью строку на (-14), а первую на 3.
Последней матрице соответствует система уравнений:
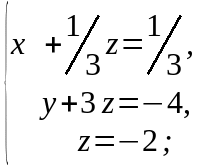
Осуществляем
обратный ход метода Гаусса. Из последнего
уравнения находим
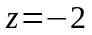 .
Подставим это значение во второе
уравнение и найдем
.
Подставим это значение во второе
уравнение и найдем
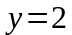 .
Далее, в первое уравнение подставляем
значения найденных неизвестных и получим
.
Далее, в первое уравнение подставляем
значения найденных неизвестных и получим
 .
.
Ответ: