Метод деления отрезком пополам

Суть метода показана на рис. 1.66. В качестве начальных данных метода задается отрезок [a,b], внутри которого расположен минимум. Отрезок [a,b] точкой с делится пополам:

с = (a + b) / 2

Вычисляются значения функции f(с – ) и f(с + ε), где ε — заданная погрешность. В зависимости от соотношения этих значений отрезок [a,b] сужается до половинного значения. Если f(с – ) < f(с + ε), то полагается b = с + ε. Если f(с – ) > f(с + ε), то отрезок сужается до а = с – . Для получившегося отрезка [a,b] вновь находится точка с и процесс продолжается до тех пор, пока b – a не окажется меньше погрешности . Минимум функции будет в точке с = (a + b) / 2.

Недостатком метода является то, что при сужении отрезка [a,b] в два раза функцию надо вычислять тоже два раза в точках f(с – ) и f(с + ε). От этого недостатка избавлен метод золотого сечения

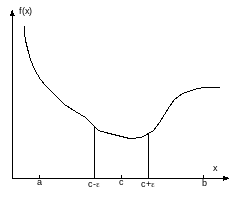
Рис. 1.66. Суть метода деления отрезка пополам

Метод золотого сечения

Суть метода показана на рис. 1.67. В качестве начальных точек задается отрезок [a,b], внутри которого расположен минимум. Отрезок [a,b] делится по правилу золотого сечения на три отрезка:

с = a + q, d = b – q,

где: q = 2 / (3 + 5^1/2) * (b – a).

Далее, как и в методе деления отрезка пополам, проверяется значения f(c) и f(d). Если f(c) < f(d), то отрезок [a,b] сужается переносом в точку b = d. При этом полагается d = c и образуется новая точка c = a + q. Если f(c) > f(d), то отрезок [a,b] сужается переносом а в точку a = c. При этом полагается c = d и образуется новая точка d = b - q. При каждом сужении отрезка [a,b] для работы метода функцию надо вычислять только один раз. Это самый эффективный метод из всех приведенных при условии, что известен отрезок [a,b] с минимумом.

Рис. 1.67. Суть метода золотого сечения

Методы вычисления корня функции одной переменной Метод простой итерации

В методе уравнение f(x) = 0 сводится к уравнению

x = x + f(x) (1)

В качестве начального приближения задается значение x_0. Далее по формуле (1) вычисляется новое значение x_1. Если |x₁ – x₀|>E (E —заданная погрешность), то полагается x₀ = x₁ и опять по формуле (1) вычисляется x₁. Процесс продолжается до тех пор пока |x₁ – x₀| не станет меньше заданной погрешности E. Корень уравнения при этом в x₁.

Недостатком метода является его плохая сходимость при произвольной функции f(x). Очень часто метод вообще не сходится к корню.

Метод деления отрезка пополам

В отличие от предыдущего метода метод гарантированно дает корень, если он имеется на заданном отрезке [a,b]. Суть метода показана на рис. 1.68. В качестве исходных данных задается отрезок [a,b] с корнем внутри его. Вычисляется функция f_a = f(a). Отрезок [a,b] делится пополам точкой c = (a + b) / 2. Вычисляется функция f_c = f(c). Далее проверяются знаки f_a и f_c. Если эти величины имеют одинаковые знаки, то точка a переносится в точку c:

a = с, f_a = f_c

_.Если f_a и f_c имеют разные знаки, то точка b переносится в точку с: b = c. Далее процесс сужения отрезка [a,b] продолжается до тех пор, пока b – a не станет меньше заданной погрешности. Корень при этом в точке с.

Рис. 1.68. Суть метода деления отрезка пополам