
- •Банк заданий дифференцированного зачета по «Математике»
- •2 Курс Специальность Сестринское дело
- •Раздел 1. Теория пределов.
- •Раздел 2. Дифференциальное и интегральное исчисление
- •Раздел 3. Дискретная математика. Теория множеств. Логика высказываний. Теория вероятности.
- •Раздел 4. Математическая статистика.
- •Раздел 5. Применение математических методов в профессиональной деятельности среднего медицинского персонала.
Банк заданий дифференцированного зачета по «Математике»
2 Курс Специальность Сестринское дело
Раздел 1. Теория пределов.
Цели: Проверить знание правил, формул и умение применять их, при вычислении пределов.
Задание 1. Среди перечисленных вариантов ответа выбрать значение предела:
1.1 |
|
а) -
б)
в) ; г) 0.
|
1.2 |
|
|
1.3 |
|
|
1.4 |
|
а) - ; б) ; в) ; г) 0. |
1.5 |
|
|
1.6 |
|
|
1.7 |
|
а) - ; б) ; в) ; г) 0. |
1.8 |
|
а) -1; б) ; в) 1; г) 0 |
1.9 |
|
|
1.10 |
|
|
1.11 |
|
|
1.12 |
|
|
1.13 |
|
а)
б) ;
в)
г) 0.
|
1.14 |
|
|
1.15 |
|
|
1.16 |
|
|
1.17 |
|
|
Раздел 2. Дифференциальное и интегральное исчисление
Цели: Проверить знание правил, формул и умение применять их, при вычислении производных, интегралов, решении дифференциальных уравнений.
Задание 1. |
Производная
функции
|
|
|
Задание 2. |
Вторая производная
функции
|
а)
б)
в)
г)
|
|
Задание 3. |
|
|
|
Задание 4. |
В результате
подстановки
|
|
|
Задание 5. |
Вычислите
|
|
|
Задание 6. |
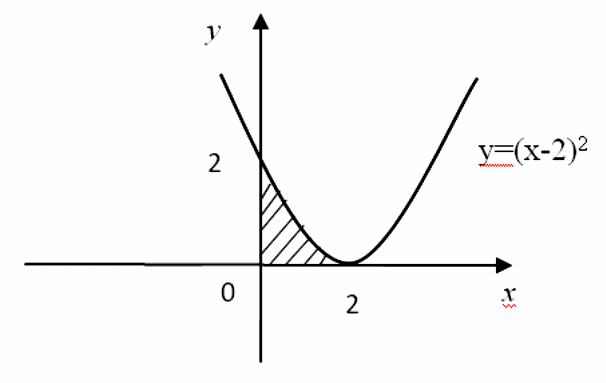
Площадь фигуры, изображенной на рисунке, определяется интегралом …
|
|
|
Задание 7. |
Производная
функции
|
|
|
Задание 8. |
Вторая производная
функции
|
а)
б)
2 в) г)
|
|
Задание 9. |
|
|
|
Задание 10. |
В результате
подстановки
|
|
|
Задание 11. |
Вычислите
|
|
|
Задание 12. |
Площадь криволинейной трапеции D определяется интегралом …
|
|
|
Задание 13. |
Производная
функции
|
|
|
Задание 14. |
Вторая производная
функции
|
а)
б)
в)
г)
|
|
Задание 15. |
|
|
|
Задание 16. |
В результате
подстановки
|
|
|
Задание 17. |
Вычислите
|
|
|
Задание 18. |
Площадь фигуры D, изображенной на рисунке, определяется интегралом …
|
|
|
Задание 19. |
Производная
функции
|
|
|
Задание 20. |
Производная
функции
|
|
|
Задание 21. |
Производная
функции
|
|
|
Задание 22. |
Вычислите
|
|
|
Задание 23. |
Вычислите
|
|
|
Задание 24. |
Вычислите
|
|
|
Задание 25. |
Производная
функции
|
|
|
Задание 26. |
Вторая производная
функции
|
а)
б)
в)
)
г)
)
|
|
Задание 27. |
Найдите все
критические точки функции y= |
|
|
Задание 28. |
В результате
подстановки
|
|
|
Задание 29. |
Вычислите
|
|
|
Задание 30. |
Площадь фигуры, изображенной на рисунке, определяется интегралом …
|
|
|
Задание 31. |
Предел
отношения приращения функции
|
||
Задание 32. |
Совокупность
всех первообразных функции
называется неопределённым … от этой
функции и обозначается
|
||
Задание 33. |
Функция
|
||
Задание 34. |
Если
производная при переходе через точку
|
||
Задание 35. |
Число А называется … величины х, если в процессе своего изменения х неограниченно приближается к А. |
||
Задание 36. |
Если производная при переходе через точку меняет свой знак с минуса на плюс, то является точкой … данной функции. |
||
Задание 37. |
Производная
произведения двух функций u
и
v
вычисляется
по формуле … в предположении, что
производные u |
||
Задание 38. |
Если функции u и v имеют в точке x производные и если v ≠ 0 , то в этой точке существует производная их частного, которая вычисляется по формуле … . |
||


 ;
;
 ;
;
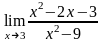
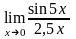 :
: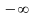 ;
;
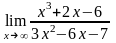 :
:
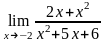
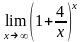
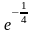 ;
;
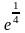 ;
;
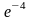 ;
;
 .
.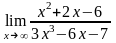 :
:


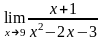
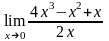
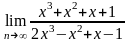
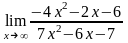
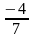 ;
;
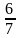 ;
;
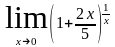
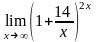

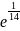
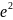
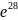
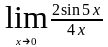
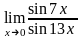
 ;
;
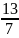 ;
;
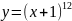 имеет вид…
имеет вид…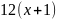
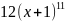
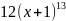
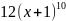
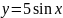 имеет вид…
имеет вид…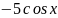
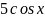

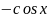
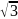 ;
;
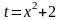 интеграл
интеграл
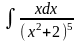 приводится к виду …
приводится к виду …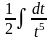



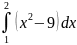 =
=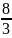

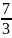
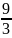

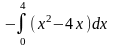
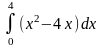
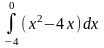
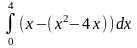
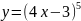 имеет вид…
имеет вид…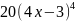
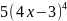
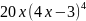
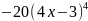
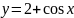 имеет вид…
имеет вид…
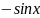
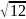 ;
-
;
-
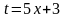 интеграл
интеграл
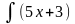
 приводится к виду …
приводится к виду …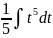
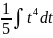

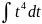

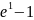

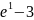
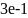

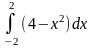
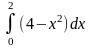
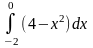

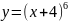 имеет вид…
имеет вид…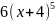

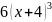
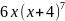
 имеет
вид…
имеет
вид…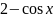

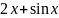
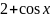
 интеграл
интеграл
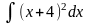 приводится к виду …
приводится к виду …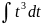
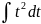
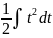

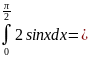

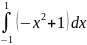
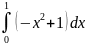
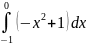
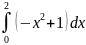
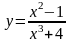 имеет вид…
имеет вид…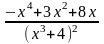

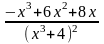

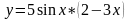 имеет вид…
имеет вид…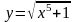 имеет вид…
имеет вид…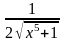

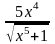
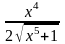
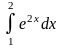
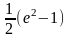
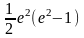



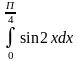
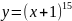 имеет вид…
имеет вид…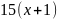
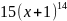


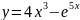 имеет
вид…
имеет
вид…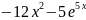

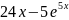
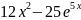

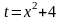 интеграл
интеграл
 приводится к виду …
приводится к виду …

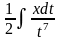
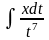
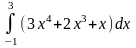
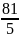
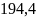
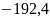

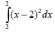
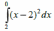
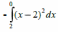
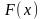 называется
… для функции
называется
… для функции
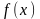 ,
если
,
если
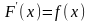 .
.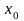 меняет свой знак с плюса на минус, то
является точкой… данной функции.
меняет свой знак с плюса на минус, то
является точкой… данной функции.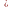 и
v
существуют.
и
v
существуют.