Ммммммннннн

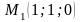, екі нүктеніің арақашықтығын тап: А) В)

нүктесінде -нің мәні, егер : А) -1

нүктесінен осіне түсірілген перпендикуляр теңдеуі:А)

екi нүктенiң арақашықтығын тап. A)5

M₀(-2;1;-1)Нүктесі арқылы өтетін S={1;-2;3}векторына параллель болатын түзудің параметрлік теңдеуі: D)x=-2+t,y=1-2t,z=-1+3tE)x+2=t,y-1=-2t,z+1=3tF)

М (1,-2,3) нүктесі арқылы өтетін және векторына перпендикуляр түзудің теңдеуі. A)

М(1;-2) нүктесінде 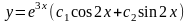- ті табыңыз, егер _. A)-1 B) -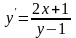

М₁(1; 1; 0), М₂(-4; 0; 3) екi нүктенiң арақашықтығын тап. А) B) C)

М₁(-1; 2; 3), М₂(3; -4; 2) екi нүктенiң арақашықтығын тап. . А) B) C)

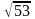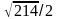М₁(3; 2; 1), М₂(4; -3; 2) екi нүктенiң арақашықтығын тап. А) B) C)

Матрицаның А₁₃ алгебралық толықтауышын есепте А) B)6

Матрицаның А₂₁ алгебралық толықтауышын есепте. А)–2 B)-4/2

Матрицаның А₂₂ алгебралық толықтауышын есепте. А)8 B)16/2

Матрицаның М₁₁ минорын тап. А)30 B)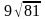

Матрицаның М₁₂ минорын тап. A) 12 B)48/4

Матрицаның М₁₃ минорын тап. A) 6 B)12/2

Матрицаның М₂₁ минорын тап. 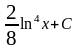A)2 B)4/2

Матрицаның рангісін анықтаңыз.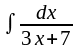 : A) B)3

Матрицаның рангы мына жағдайларда өзгермейді: А) Кез-келген екі жолын (бағанын)) ауыстырғанын. В) Кез-келген жолының (бағанының) элементтерін санына көбейткеннен. С) Кез-келген қатардың элементтерін санына көбейтілген басқа қатардың элементтерін қосқаннан.

Матрицаның рангы мына жағдайларда өзгермейді: А) Кез-келген жолының (бағанның) элементтерін санына көбейткеннен. В) Кез-келген элементтерін басқа сандармен ауыстырғаннан. С) Кез-келген элементтеріне санына көбейтілген басқа қатардың элементтерін қосқаннан.

Матрицанынң рангы мына жағдайларда өзгермейді: C)кез келген жолының бағанының элементтерін санына көбейткеннен E)кез-келген екі жолын бағанын ауыстырғаннан

Мына матрицаүшін кері матрицаны табуға болады:B) E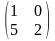

Мына матрица үшін кері матрицаны табуға болады: А) В) С)

Мына өлшемді матрицалардың көбейтіндісін табуға болады: B) және

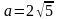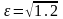Нақты осі , ал эксцентриситеті болатын гипербола теңдеуі А) В)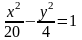

Нақты осі , ал эксцентриситеті болатын гипербола теңдеуі:A)

Негізгі интегралдар кестесінің формуласы:E)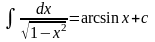 G)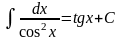

ООООООООРРРРРР

Ойын сүйегі лақтырылды. Жұп ұпайлар түсу ықтималдығын табыңыз: A)0,5 B)1/2

Ойын сүйегі лақтырылды. Тақ ұпайлар түсу ықтималдығын табыңыз: A)0,5 B)1/2

Орташа квадраттық ауытқу тең болса, онда дисперсияны табыңыз. A) B) C)36

параболасы үшін:А) төбесі

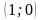
Радиусы , центрі нүктесінде жатқан шеңбердің теңдеуі:А) В) С)

СССССССТТТТТТТ

Скаляр көбейтіндінің қасиеттері А) В)

Скалярлық көбейтіндісінің қасиеттері:A) B) D)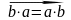

Сызықтармен шектелген фигураның ауданын табу керек , , , А)8/2 В)4 С) 12/3

Сызықтармен шектелген фигураның ауданын табу керек , , , А) 1В) 8/8

Сызықтармен шектелген фигураның ауданын табу керек А) 128/2 В) 192/3 С) 64

Сызықтармен шектелген фигураның ауданын табу керек А) 30/5В) 6

Сызықтармен шектелген фигураның ауданын табыңыз: A) 1 B)2/2

Сызықтармен шектелген фигураның ауданын табыңыз: A) 35 B)70/2

Сызықтармен шектелген фигураның ауданын табыңыз: A) 48

Сызықтармен шектелген фигураның ауданын табыңыз: A) 6 B)18/3

Сызықтармен шектелген фигураның ауданын табыңыз: A) 9

Сызықтармен шектелген фигураның ауданын табыңыз: y=5x, x=2, y=0 A) 10

Сызықтармен шектелген фигураның ауданын табыңыз: A) 2

Сызықтармен шектелген фигураның ауданын табыңыз: A) 8

Сызықтармен шектелген фигураның ауданын табыңыз: A) 9

Сызықтармен шектелген фигураның ауданын табыңыз: A) 8

Тақ функция А)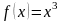 В)

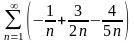Таңбалары айнымалы қатар:А) В) С)

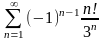
Таңбалары айнымалы қатар:С)

Теңдеуді шешіңіз: . A) B) C)

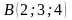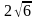Төбелері , және нүктелері болатын үшбұрыштың ауданы тең: D) Е) F)

Тікелей интегралдау арқылы табылатын интеграл: A) 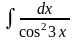B) E)

Төбелері A(3;-3;1), B(5;-2;3) және C(3;-1;3) болатын үшбұрыштың ауданы жататын аралық:D)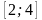 E)