
Двоичные сумматоры - вычитатели

Теперь, когда мы знаем, что двоичные сумматоры можно использовать как для сложения, так и для вычитания, спроектируем схему универсального устройства – сумматора - вычитателя, положив в ее основу схему вычитателя (рис. 4, б). Чтобы эта схема работала как 3-разрядный сумматор, достаточно временно (условно) исключить из нее 3 инвертора и на вход переноса младшего разряда подать “0”. В преобразованном виде эта схема (рис. 5) вместо инверторов содержит три логических элемента М2 (сумма по модулю 2). При подаче 0 на вход V логического элемента М2 информационные биты каждого разряда двоичного числа b2b1b0 проходят через этот элемент без инверсии. Таким образом, при установке 0 на управляющем входе схема складывает двоичные числа a2a1a0 и b2b1b0. Результат появляется на выходных индикаторах. Кроме того, логический 0 на управляющем входе V поступает на вход переноса младшего разряда двоичного сумматора.
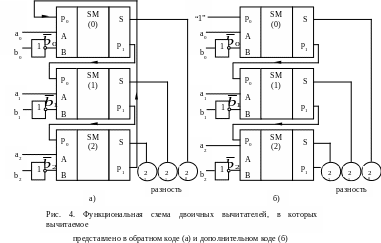
Чтобы схема работала как 3-разрядный вычитатель, на управляющем входе V нужно установить уровень логической 1. В этом случае логический элемент М2 действует как инвертор сигналов на входах B одноразрядных сумматоров. Кроме того, логическая 1 на управляющем входе поступает на вход переноса младшего разряда двоичного сумматора.
Сумматоры
Каким образом выполняется суммирование двух положительных чисел в двоичном коде? Например, 3+5=8:
1 1
0011
+0101
1000.
Существует большое многообразие сумматоров в [4] приведено 9 типов сумматоров, рассмотрим самые простые из них.
Таблица 1 – Таблица истинности для полного сумматора
a |
b |
Cin |
S |
Cout |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
![]() .
.
Выполнив минимизацию Cout по карте Карно, получим;
![]() .
.
Сin – перенос из предыдущего младшего разряда,
Cout – перенос с следующий старший разряд.
На рисунке 1 представлена схема одноразрядного полного сумматора.
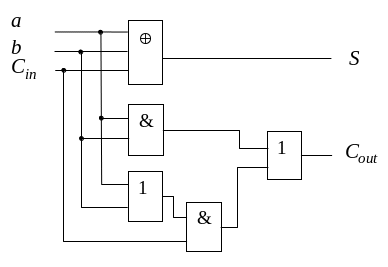
Рисунок 1 – Схема одноразрядного полного сумматора
Для последовательного выполнения операции сложения (разряд за разрядом) используется один полный сумматор, общий для всех разрядов. Для выполнения операции операнды и перенос подаются на него последовательно, начиная с младших разрядов рисунок 2.
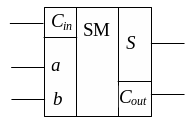
Рисунок 2 – Схема последовательного сумматора
Последовательный сумматор имеет небольшие аппаратурные затраты, но требует большого времени выполнения операции. Более быстродействующим будет параллельный сумматор с последовательным переносом. Для примера рассмотрим четырехразрядный параллельный сумматор с последовательным переносом (рисунок 3).
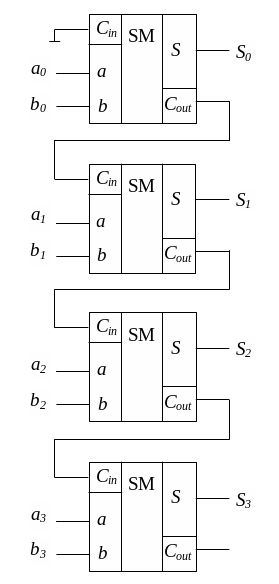
Рисунок 3 – Схема параллельного сумматора с последовательным переносом
Для каждого разряда в этой схеме используется отдельный одноразрядный полный сумматор. В младший разряд (a0, b0) переноса нет, поэтому Сin=0. На каждый последующий разряд подеется перенос из предыдущего. Хоть сумматор и называется параллельным, на самом деле все разряды обрабатываются не точно одновременно, а только после формирования переноса для данного разряда. Отсюда следует, что быстродействие устройства определяется суммой задержек передачи сигнала переноса с младшего разряда на выход сумматора старшего разряда.
