Цифровые компараторы

Компаратором (устройством сравнения) называют функциональный узел, обеспечивающий сравнение двух чисел А и В. Если А и В – n-разрядные двоичные числа, то компаратор именуют цифровым.

Простейшие компараторы формируют на выходе однобитовый сигнал равенства, или неравенства сравниваемых чисел А и В. Эти отношения используются как логические условия в микропрограммах, в устройствах контроля и диагностики ЭВМ, в устройствах автоматики компараторы используются для сигнализации о выходе величин за установленные пределы и т.д.

Компараторы строятся на основе поразрядных операций над одноименными разрядами обоих слов. Слова равны, если попарно равны все одноименные их разряды. Признак (условие) равенства i-х разрядов сравниваемых слов А и В:

(1)

Условие неравенства i-x разрядов:

(2)

Схемная реализация приведенных условий изображена на рис. 1, а.

Схема n-разрядного компаратора на равенство показана на рис.1, б.

Более сложные компараторы выявляют не только факт равенства двух n-разрядных чисел, но и сравнивают числа по значению. Такие компараторы имеют три выхода: “A>B”, “A=B”, “A<B”, и в зависимости от соотношения величин А и В активный уровень (- уровень логической 1) появляется на одном из этих выходов.

Построить такой компаратор можно на базе двоичного сумматора, выполнив на нем операцию вычитания А-В и проанализировав полученный результат. Для этого на сумматор нужно число В подать в дополнительном коде (см. лабораторную работу №4 “Двоичные сумматоры”). Тогда выходной перенос сумматора (р₁) будет равен 0 лишь в том случае, когда А строго меньше В. Равенство разности 0 является признаком того, что А=В. Единица переноса при нулевой сумме указывает на то, что А строго больше В. Сказанное иллюстрируют следующие примеры:

Примечание. Вычитание из числа А числа В=12₁₀=1100₂ заменено прибавлением к А дополнительного кода числа В, равного 0100₂.

Правила справедливы, если числа А и В рассматриваются как положительные величины, без знака. Если же их старшие разряды трактуются как знаки, то правила будут несколько иные. Их легко вывести самостоятельно, если есть навыки обращения с обратными и дополнительными кодами.

Схема, реализующая описанный алгоритм, изображена на рис. 2.

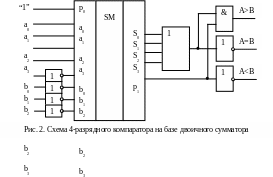
Примером компаратора двоично-кодированных чисел может служить ИС 4-разрядного компаратора К555СП1 (рис. 3). Компаратор имеет 11 входов. Четыре пары входов а_i b_i (i=0,1,2,3) используются для подачи на них соответствующих разрядов сравниваемых чисел, входы A<B, A=B, A>B позволяют каскадировать несколько ИС компараторов для увеличения разрядности сравниваемых чисел. Компаратор имеет три выхода результатов сравнения: A>B, A=B и A<B. При каскадировании выходы A>B, A=B и A<B схемы, сравнивающей младшие разряды, следует присоединить к одноименным входам последующего каскада. Этим способом с помощью двух компараторов СП1 можно сравнивать два восьмиразрядных слова. Нетрудно подсчитать необходимое число каскадов для любой большей д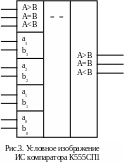 лины сравниваемых слов.

Все возможные комбинации поразрядных соотношений входных кодов, а также уровней на входах каскадирования сведены в таблицу, где показаны соответствующие результирующие уровни на выходах A>B, A=B и A<B (табл. 1).

Таблица 1

Входы сравнения данных				Входы наращивания каскадов			Выходы
a3, b3	a2, b2	a1, b1	а0, b0	I(A>B)	I(A<B)	I(A=B)	A>B	A<B	A=B
a3>b3	x	х	x	x	x	x	B	H	H
a3<b3	х	х	x	x	x	x	H	B	H
a3=b3	a2>b2	х	x	x	x	x	B	H	H
a3=b3	a2<b2	х	x	x	x	x	H	B	H
a3=b3	a2=b2	a1>b1	x	x	x	x	B	H	H
a3=b3	a2=b2	a1<b1	x	x	x	x	H	B	H
a3=b3	a2=b2	a1=b1	a0>b0	x	x	x	B	H	H
a3=b3	a2=b2	a1=b1	a0<b0	x	x	x	H	B	H
a3=b3	a2=b2	a1=b1	a0=b0	H	H	B	H	H	B