Лабораторная работа №5

Моделирование проблем ракетостроения.

1. Постановка задачи

   1. Описание эксперимента

Эксперимент по моделированию проблем ракетостроения состоит в определении нужных условий, для успешного запуска ракеты на орбиту. В первом эксперименте, мы рассчитаем, какую максимальную скорость сможет развить одноступенчатая ракета. Во втором – многоступенчатая.

2. Моделирование Эксперимента

   1. Объект исследования

Объектом исследования является эксперимент по запуску ракеты на орбиту Земли.

2. Упрощения

Для упрощения математической модели мы не будем учитывать силу сопротивления воздуха и гравитации.

3. Математическая модель №1

Создадим модель ракеты. Зададим ее основные параметры: u - скорость истечения сгорающего топлива (3 км/с); m0 - масса ракеты на старте; mp - "полезная" нагрузка; lambda - коэффициент структурной массы (ms). Тогда структурная масса ракеты будет равна ms=lambda*m0, а масса топлива mt=m0-ms-mp. Исходя из закона сохранения импульса, получим формулу зависимости скорости от сгоревшего топлива. V=u*ln(m0./(m0-mtt))

1. Визуальное представление

Чтобы наглядно продемонстрировать полученную зависимость скорости от сгоревшего топлива, воспользуемся функцией Matlab plot().

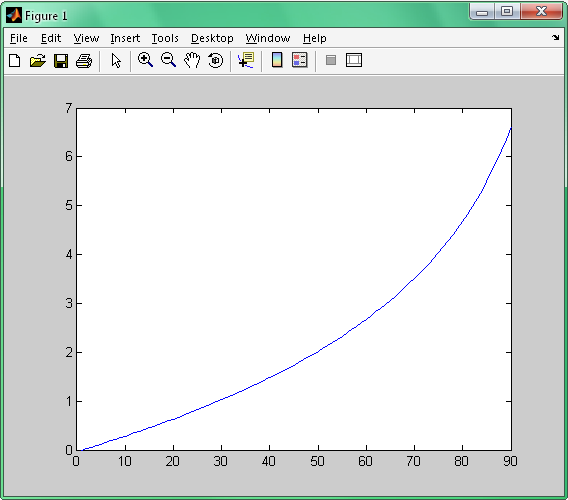
m0=1.2;mp=0.1;lambda=0.1

На данном графике легко увидеть, что ракета не сможет развить скорость больше 7км/c. Т.к. 1 космическая скорость равна 8 км/c то такая ракета, никогда не выйдет на орбиту. Даже при уменьшении полезной нагрузки на несколько порядков, скорость меняется не значительно. Лишь при уменьшении коэффициента lambda можно достигнуть скорости более 8 км/c, но это нам не подходит. Решением этой проблемы является использование нескольких ступеней.

4. Моделирование эксперимента №2.

К уже существующей модели одноступенчатой ракеты добавим лишь число ступеней равное 3. mi – масса i-ой ступени. msi – структурная масса i-ой ступени. Исходя из закона сохранения импульса, получим формулу зависимости скорости от сгоревшего топлива для 2 ступени: v=v1+ +u*ln((m0-m1)./(m0-m1-mtt2)); для 3 ступени v=v2+ u*ln((m0-m1-m2)./(m0-m1-m2-mtt3)); где mtt2(3) – масса сгоревшего топлива. Для 2(3) ступени. Таким образом мы получили зависимость скорости ракеты от массы топлива.

1. Визуальное представление.

Как и в предыдущем примере построим получившуюся зависимость в виде графика.

Из рисунка видно, что конечная скорость ракеты превышает первую космическую, а значит, что ракета выйдет на орбиту, более того во 2 случае общая масса ракеты будет такой же как и в первом, а это значит топливо будет тратится эффективней.

3. Приложение

Exp1.m

m0=1;mp=0.01;lambda=.1;ms=m0*lambda;mt=m0-mp-ms;

[m0 mt ms mp]

mtt=0:.01:mt;

u=3;v=u*log(m0./(m0-mtt));

plot(v)

Expr2.m

m0=1;mp=0.01;lambda=.1;

mi1=0.39;mi=0.3;

ms1=lambda*mi1;

ms=lambda*mi;

[m0 mt ms mp]

mtt=0:0.01:(0.39-ms1);

u=3;

v=u*log(m0./(m0-mtt));

v1=max(v);

mtt2=0.01:0.01:(0.3-ms);

v2=v1+u*log((m0-mi1)./(m0-mi1-mtt2));

v20=max(v2);

mtt3=0.01:0.01:(0.3-ms);

v3=v20+u*log((m0-mi1-mi)./(m0-mi1-mi-mtt2));

v=[v v2 v3];

plot(v)