Моделирование проблем ракетостроения.

1. Постановка задачи Теория

   1. Принципы и законы

Принцип реактивного движения положен в основу многих заме­чательных технических устройств, например, ракеты, выводящей на орбиту вокруг Земли искусственный спутник, для чего ей требуется развить скорость примерно 8 км/с. Простейшая математическая мо­дель движения ракеты получается из закона сохранения импульса в пренебрежении сопротивлением воздуха, гравитацией и другими си­лами, исключая, конечно, тягу реактивных двигателей.

Пусть продукты сгорания ракетного топлива покидают располо­женные в кормовой части выхлопные сопла со скоростью u (для со­временных топлив величина и равна 3-5 км/с). За малый промежуток времени dt между моментами t и t+dt часть топлива выгорела, и масса ракеты изменилась на величину dm. Изменился также импульс ракеты, однако суммарный импульс системы «ракета плюс продукты сгорания» остался тем же, что и в момент t, т. е.

m(t) v(t) = m(t + dt) v(t + dt) - dm [v(t + ξdt) - u],

где v(t) — скорость ракеты, v(t + ξdt) — и, 0 < ξ < 1 — средняя за про­межуток dt скорость истекающих из сопел газов (обе скорости берутся относительно Земли). Первый член в правой части этого равенства — импульс ракеты в момент t + dt, второй — импульс, переданный исте­кающим газом за время dt.

Учитывая, что m(t + dt) = m(t) + (dm/dt) dt + 0(dt2), закон сохра­нения импульса можно переписать в виде дифференциального уравне­ния:

m*(dv/dt)=-dm/dt*u

в котором член - (dm/dt) и, очевидно, не что иное, как сила тяги ра­кетных двигателей, и которое, будучи преобразованным к виду:

dv/dt=-u(d(ln m)/dt)

легко интегрируется:

v(t) = V0 + u ln(m0/m(t))

где v0,m0 — соответственно скорость и масса ракеты в момент t = = 0. Если v0 = 0, то максимальная скорость ракеты, достигаемая при полном сгорании топлива, равна

v = u ln(m0/( mp+ ms)) (*)

Здесь mp — полезная масса (масса спутника), ms — структурная масса (масса собственно ракетной конструкции — топливных баков, двига­телей, систем управления и т. д.).

2. Формула Циолковского

Формула (*) позволяет сделать фундамен­тальный вывод о конструкции ракеты для космических полетов. Введем величину λ =ms/(m0-mp), которая характеризует при m0=0 отношение структурной и начальной масс ракеты. Тогда для практически реальных значений λ = 0.1, u= 3 км/с получаем при mp = 0

v = u ln(l/λ) = 7 км/с.

Отсюда следует, что даже в самой идеальной ситуации (полезная масса равна нулю, отсутствуют гравитация и сопротивление возду­ха и т. д.) ракета рассматриваемого типа не способна достичь первой космической скорости. Тем самым необходимо использовать многосту­пенчатые ракеты — вывод, к которому пришли основоположники кос­монавтики.

2. Моделирование Эксперимента

   1. Исследование одноступенчатой ракеты.

%полезная масса

mp=10;

%масса ракеты на старте

m0=1000;

%коэффициент структурной массы

lambda=0.1;

%Скорость сгорания топлива

u=3000;

%Массa топлива

mt0=m0-lambda*m0;

%структурная масса

ms=m0*lambda;

%массив cгорания топлива

mtt0=0:10:mt0;

%Скорость по закону Циалковского

v1=u*log(m0./(m0-mtt0));

%Построение графика

plot(mtt0,v1,'k-')

2. Исследование многоступенчатой ракеты.

mp=0.01;

m1=0.33; m2=0.33; m3=0.33;

m0=mp+m1+m2+m3;

lambda=0.1;

%Скорость сгорания топлива

u=3000;

%Массы топлива

mt1=m1-lambda*m1;

mt2=m2-lambda*m2;

mt3=m3-lambda*m3;

%массивы cгорания топлива

mtt1=0:.01:mt1;

mtt2=0:.01:mt2;

mtt3=0:.01:mt3;

%Скорости по закону Циалковского для 3-ех ступеней.

v1=u*log(m0./(m0-mtt1));

v2=v1(1)+u*log((mp+m2+m3)./(mp+m2+m3-mtt2));

v3=v2(1)+u*log((mp+m3)./(mp+m3-mtt3));

%Построение графика

axis([0 1000 0 10000]);

hold on;

grid on;

j=1;

k=1;

p=1;

for i=0:.01:(mt1+mt2+mt3)

if(i<mt1)

plot(1000*i,v1(k),'y.')

k=k+1;

else

if (i<(mt1+mt2))

plot(1000*i,v2(p)+v1(k-1),'g.')

p=p+1;

else

plot(1000*i,v3(j)+v1(k-1)+v2(p-1),'r.')

j=j+1;

end

end

end

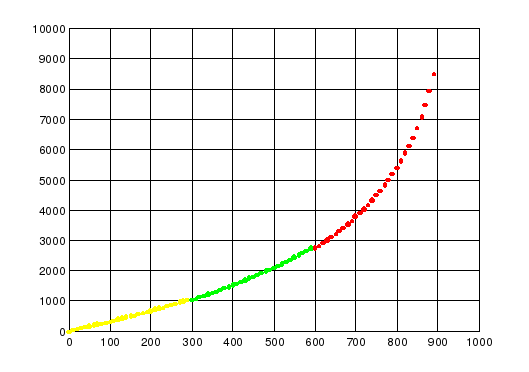
3. Выводы

Как видно из результатов даже при самой идеальной ситуации (нет полезной массы) одноступенчатая ракета не способна достичь первой космической скорости.

Решение проблемы - использовние многоступенчатых ракет.