Лабораторная работа №5

Моделирование проблем ракетостроения.

Объект исследования.

В данной работе исследуются модели одноступенчатой и многоступенчатой ракеты. Меняя различные параметры ракеты мы будем получать ее скорость.

Упрощающие предположения.

Простейшая математическая модель движения ракеты получается из закона сохранения импульса в пренебрежении сопротивлением воздуха, гравитацией и другими силами, исключая тягу реактивных двигателей.

Часть 1. Исследование полета одноступенчатой ракеты.

Теоретическая часть.

Зададим переменные:

u - скорость истечения сгорающего топлива (3 км/с);

m0 - масса ракеты на старте;

v0 – начальная скорость ракеты (на старте = 0);

mp - "полезная" нагрузка;

λ (lambda) - коэффициент структурной массы (ms);

v - скорость ракеты;

mt - массу топлива;

Закон сохранения импульса в виде дифференциального уравнения:

;

Преобразовываем к виду:

;

После интегрирования получаем формулу Циолковского:

, где m(t) = mp + ms;

;

Математическая модель эксперимента.

Для построения модели одноступенчатой ракеты в MATLAB напишем следующий код, основываясь на теоретических сведениях, изложенных ранее:

>> m0=1;

>> mp=.01;

>> lambda=.1;

>> ms=m0*lambda;

>> mt=m0-mp-ms;

>> [m0 mt ms mp]

ans =

1.0000 0.8900 0.1000 0.0100

>> mtt=0:.01:mt;

>> u=3;

>> v=u*log(m0./(m0-mtt));

>> plot(v)

В результате получим следующий график:

Рисунок 1. График изменения скорости в зависимости от потери массы.

Вывод.

Даже при самой идеальной ситуации (нет полезной массы) ракета рассматриваемого типа не способна достичь первой космической скорости.

Часть 2. Исследование полета многоступенчатой ракеты.

Для того, чтобы достичь первой космической скорости при движении ракеты необходимо избавляться от балласта: отработавшей части структурной массы. Многоступенчатая ракета состоит из нескольких ступеней, отбрасываемых по мере их использования.

Зададим переменные:

mi – общая масса i-й ступени;

λmi – соответствующая структурная масса;

mp – масса полезной нагрузки;

u – скорость истечения газов;

v – скорость ракеты;

Рассмотрим зависимость для трех ступеней.

Начальная масса ракеты m0 = mp + m1+ m2 + m3.

По формуле Циолковского скорость ракеты, после достижения которой структурная масса отбрасывается и включается вторая ступень:

;

Для окончательной скорости имеем:

,

где α1 = , α2= , α3 = ;

v3 = uf(α1, α2, α3) – максимум функции f достигается в симметричном случае, т.е. при α1 = α2 = α3 = α

;

;

Для моделирования данной зависимости в программе использовался следующий код:

>> V = 8;

>> n = 2;

>> lambda = 0.1;

>> u = 3;

>> mp = 0.1;

>> P = exp(-V/(n*u));

>> alpha = ((1-lambda)/(P-lambda));

>> m3 = (alpha-1)*mp;

>> m2 = (mp+m3)*alpha-(mp+m3);

>> m0 = alpha*(mp+m2+m3);

>> m1 = m0-m2-m3;

>> mt1 = (1-lambda)*m1;

>> mt2 = (1-lambda)*m2;

>> mt3 = (1-lambda)*m3;

>> mtt1 = mt1:-.001:0;

>> mtt2 = mt2:-.001:0;

>> mtt3 = mt3:-.001:0;

>> v1 = u*log(m0./(m0-mtt1));

>> v2 = v1(1) + u*log((mp+m2+m3)./(mp+m2+m3-mtt2));

>> v3 = v2(1) + u*log((mp+m3)./(mp+m3-mtt3));

>> axis([0 10 0 12]);

>> hold on;

>> xlabel('mass');

>> ylabel('speed');

>> i = 1;

>> j = 1;

>> k = 1;

>> for m = 0:0.001:(mt1+mt2+mt3)

if(m < mt3)

plot(m, v3(i), 'r');

i = i+1;

else

if(m < mt2+mt3)

plot(m, v2(j), 'y');

j = j+1;

else

plot(m, v1(k), 'k');

k = k+1;

end

end

end

В результате выполнения следующего кода получаем следующие графики:

Рисунок 2. График при n=2.

Рисунок 3. График при n=3.

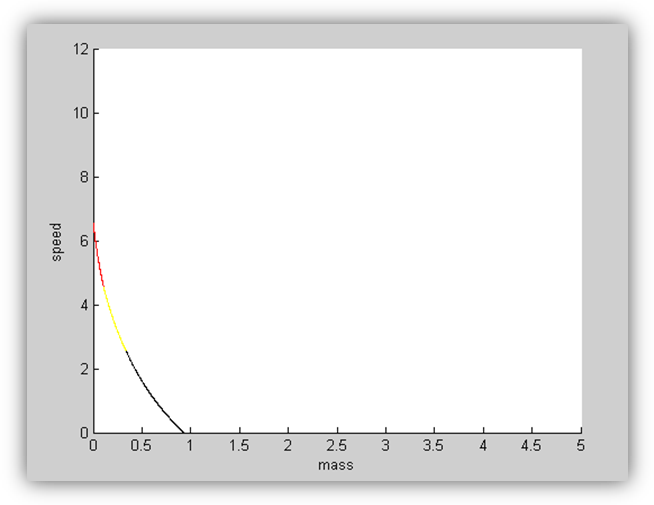
Рисунок 4. График при n=4.

Вывод.

Из графиков видно, что при увеличении числа ступеней ракеты увеличивается и масса ракеты. Для двухступенчатой ракеты при массе 0.1 тонна полезного груза необходимо иметь массу ракеты весом 5 тонн. Переход к третьей ступени уменьшает массу ракеты, причем значительно: примерно 2.1 тонны. А у четырехступенчатой ракеты: примерно 1 тонна, что не дает заметного выигрыша по сравнению с трехступенчатой.