Лабораторная работа №5

Моделирование проблем ракетостроения.

1. Объект исследования

Исследование одноступенчатой ракеты. Исследование полета многоступенчатой ракеты.

2. Упрощения

Мы пренебрегаем сопротивлением воздуха, гравитацией и другими силами, исключая тягу реактивных двигателей.

3. Ход эксперимента

   1. Описание математической модели.

      1. Одноступенчатая ракета

Пусть продукты сгорания ракетного топлива покидают расположенные в кормовой части выхлопные сопла со скоростью u. За малый промежуток времени dt между моментами t и t+dt часть топлива выгорела, и масса ракеты изменилась на dm.

Применим закон сохранения количества движений:

,

где - скорость ракеты, - средняя за промежуток времени dt скорость истекающих из сопел газов (обе скорости берутся относительно Земли).

Также, по формуле Тейлора имеем:

.

Подставив данные выражения в наше уравнение, получаем:

с точностью до членов более высокого порядка малости, чем dt.

Раскроем скобки:

- дифференциальное уравнение для .

Чтобы получить задачу Коши, нам нужно добавить начальные условия:

.

Получаем задачу Коши:

Получаем:

- скорость ракеты в момент времени t.

Посмотрим, какую максимальную скорость может развить одноступенчатая ракета:

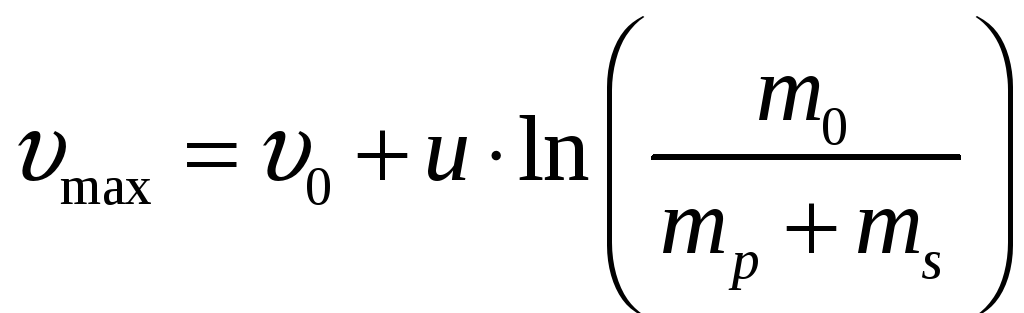, так как стартовая скорость нашей ракеты равна 0, то имеем:

.

Примем полезную массу равной 0, а , u=3км/сек. Получаем:

.

Следовательно, на одноступенчатой ракете не возможно вылететь в космос, т.к. для этого нам нужно иметь скорость больше первой космической (7,9 км/сек).

2. Многоступенчатая ракета

Как мы уже установили, реальная одноступенчатая ракета неспособна развить первую космическую скорость. Это происходит из-за затрат горючего на разгон ненужной, отработавшей части структурной массы. Следовательно, при движении ракеты необходимо периодически избавляться от балласта. Т.е. ракета должна состоять из нескольких ступеней, отбрасываемых по мере их использования.

Пусть - общая масса i-ой ступени, - соответствующая структурная масса (при этом масса топлива равна величине ), - масса полезной нагрузки. Для простоты допустим, величины и скорость истечения газов u одинаковы для всех ступеней.

Рассмотрим 3-ёх ступенчатую ракету.

Начальная масса такой ракеты будет вычисляться по формуле:

.

Рассмотрим момент, когда израсходовано всё топливо первой ступени и масса ракеты равна величине:

.

Тогда по формуле для скорости одноступенчатой ракеты имеем:

.

После достижения этой скорости (), структурная масса () отбрасывается и включается вторая ступень. Масса ракеты в этот момент равна

.

После выгорания топлива во второй ступени скорость ракеты равна:

.

Аналогично, после сгорания топлива в 3-ей ступени, скорость ракеты равна:

.

Подставляя эти формулы, друг в друга, получаем:

, или, вводя величины , , получаем:

.

Исследуем эту формулу, найдём при каких значениях , она будет принимать максимальное значение.

Для того, чтобы натуральный логарифм был максимальным нам необходимо, чтобы знаменатель аргумента логарифма был максимальным, т.е. значение аргумента логарифма было как можно меньше 1 и ближе к 0.

==

=

.

Так как , , , , получаем:

, это выражение должно быть минимальным, а для этого нам необходимо, чтобы сумма была максимальной, а это при .

Формула будет выглядеть:

Аналогичный результат получаем для n ступеней:

.

Получаем:

, , .

2. Реализация математической модели.

   1. Одноступенчатая ракета

Для реализации математической модели используем программу MatLab.

Построим график изменения скорости ракеты, от количества сгоревшего топлива.

Создадим процедуру lab_05_01.m:

m0=1; % задаём полную массу ракеты

mp=.01; % задаём полезную массу ракеты

lambda=.1; % задаём коэффициент структурной массы ракеты

ms=m0*lambda; % вычисляем структурную массу ракеты

mt=m0-mp-ms; % масса ракеты в зависимости от времени

[m0 mt ms mp]

mtt=0:.01:mt; % задаём разные значения массы ракеты в процессе полёта

u=3; % задаём скорость покидания сгоревшего топлива из сопел

v=u*log(m0./(m0-mtt)); вычисляем скорость ракеты в зависимости от массы

plot(v) % строим график зависимости скорости ракеты от массы

Получаем график изображённый на рисунке (Рис. 1):

Рис. 1

2. Многоступенчатая ракета

Для реализации математической модели используем программу MatLab.

Построим график изменения скорости ракеты, от количества сгоревшего топлива.

Создадим процедуру lab_05_02.m:

clear

m0=input('Vvedite m0 ') % вводим массу ракеты

mp=input('Vvedite mp ') % вводим полезную массу ракеты

alfa=(m0/mp)^(1/3) % рассчитываем альфа (см. мат. модель)

m3=(alfa-1)*mp % рассчитываем массу 3-ей ступени

m2=(alfa-1)*mp+(alfa-1)^2*m3 % рассчитываем массу 2-ой ступени

m1=m0-m2-m3-mp % рассчитываем массу 1-ой ступени

lambda=.1; % задаём коэффициент статической массы ракеты

m11=fix((m1-m1*lambda)*100) % масса топлива в 1-ой ступени

m22=fix((m2-m2*lambda)*100) % масса топлива во 2-ой ступени

m33=fix((m3-m3*lambda)*100) % масса топлива в 3-ей ступени

u=3; % скорость выхода из сопел отработавшего горючего

v1=zeros(1,m11+m22+m33); % создаём матрицу, куда будем записывать скорость

for n=1:1:m11; % рассчитываем

mtt=n/100; % скорость во время работы

v1(n)=u*log(m0/(m0-mtt)); % 1-ой ступени

end

for n=1:1:m22; % рассчитываем

mtt=n/100; % скорость во время работы

v1(n+m11)=v1(m11)+u*log((m0-m1)/(m0-mtt-m1)); % 2-ой ступени

end

for n=1:1:m33; % рассчитываем скорость во время работы

mtt=n/100; % 3-ей ступени

v1(n+m11+m22)=v1(m11+m22)+u*log((m0-m1-m2)/(m0-mtt-m1-m2));

end

plot(v1, 'r-') % рисуем график зависимости скорости

% от величины сгоревшего топлива

Получаем результат в виде графика (Рис. 2, Рис. 3):

Рис. 2

Мы ввели значения:

m0=10; mp=0.417.

Рис. 3

Мы ввели значения:

m0=10; mp=0.125.

Создадим процедуру lab_06_02.m:

сlear % очищаем значения переменных

vn=10.5; % задаём значение скорости до которой нужно разогнать ракету

u=3; % задаём скорость покидания сгоревшего топлива из сопел

lambda=0.1; % задаём коэффициент структурной массы ракеты

for n=2:1:10 % создаём цикл, n – кол-во ступеней у ракеты

P(n)=exp((-vn)/(n*u)) % см. Мат. модель

k(n)=((1-lambda)/(P(n)-lambda))^n % коэфф. m0/mp

end % заканчиваем цикл

u=4; % задаём скорость покидания сгоревшего топлива из сопел

for n=2:1:10 % создаём цикл, n – кол-во ступеней у ракеты

P1(n)=exp((-vn)/(n*u)) % см. Мат. модель

k1(n)=((1-lambda)/(P1(n)-lambda))^n % коэфф. m0/mp

end % заканчиваем цикл

u=5; % задаём скорость покидания сгоревшего топлива из сопел

for n=2:1:10 % создаём цикл, n – кол-во ступеней у ракеты

P2(n)=exp((-vn)/(n*u)) % см. Мат. модель

k2(n)=((1-lambda)/(P2(n)-lambda))^n % коэфф. m0/mp

end % заканчиваем цикл

plot(k, 'g*')

hold

plot(k, 'g-') % Выводим полученные

plot(k1, 'r*') % результаты

plot(k1, 'r-') % в виде графиков

plot(k2, '*')

plot(k2, '-')

Получаем результат в виде графика (Рис. 4):

Рис. 4

На данном графике изображена зависимость соотношений масс (общей массы ракеты, к массе полезной) от количества ступеней у ракеты, для разгона ракеты до скорости 10.5 км/сек.

* - ми обозначены рассчитанные значения (естественно 3,5 ступени мы сделать не можем, но для наглядности соединяем эти точки).

Соотношений масс показывает нам, сколько тон должна весить ракета, чтобы вывести полезный груз массой одна тонна на орбиту.

Например, для выведения полезного груза массой 1 тонна, с помощью двухступенчатой ракеты, она должна весить 149 тонн.

Построим такие же графики, для разгона ракеты до скорости 8 км/сек. Для этого в процедуре, поменяем значении скорости vn, на 8 км/сек.

Получаем результат в виде графика (Рис. 5):

Рис. 5

4. Вывод

   1. Одноступенчатая ракета

Мы получили, что даже в самой идеальной ситуации (полезная масса равна нулю, отсутствует гравитация и сопротивление воздуха и т.д.) ракета одноступенчатого типа не способна достичь первой космической скорости. По нашим расчётам, получилось, что максимальную скорость, которую может развить одноступенчатая ракета, равна:

2. Многоступенчатая ракета

Зависимости соотношения масс от количества ступеней у ракеты изображены на Рис. 4 и Рис. 5.

Глядя на зависимости соотношения масс от количества ступеней, можно сказать, что чем больше u (скорость покидания продуктов сгорания из сопел двигателя) тем меньше влияет количество ступеней. Так же по графику хорошо видно, что 6-и ступенчатая ракета не даёт заметного выигрыша по сравнению с 5-и ступенчатой. В принципе после 3 ступени он уже не очень существенный. Из этого мы можем сделать вывод, что оптимальное количество ступеней у ракеты, это 3.