Лабораторная работа № 3

Статистическое моделирование лекционного эксперимента с совпадающими днями рождения студентов групп МП-30, МП-34, МП-35

1. Объект исследования

Объектом исследования является парадокс дней рождения. Парадоксальным является утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек, превышает 50 %. Для 60 и более человек вероятность такого совпадения превышает 99 %, хотя 100 % она достигает только когда в группе не менее 366 человек (или не менее 367 человек, если год високосный). Но это утверждение не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.

2. Упрощающие предположения

Для построения математический модели предположим, что дни рождения распределены равномерно, нет високосных лет, близнецов, рождаемость не зависит от дня недели, времени года и других факторов.

3. Теоретический расчет

Постановка задачи: какова вероятность того, что в группе из n (n<=365) случайно отобранных студентов хотя бы у двоих окажется один и тот же день рождения?

Событие А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}.

Вероятность события А определяется по формуле классической вероятности: , где - число всех благоприятствующих событию А исходов, - число всех исходов эксперимента.

Очевидно, что гораздо удобнее сначала вычислить вероятность события ={ни у кого из студентов не совпадут дни рождения}, а затем события А.

Таким образом вероятность события A вычисляется по формуле

4. 1-й вариант эксперимента

Исследуем вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}.

Пусть n – число участников эксперимента, N – число опытов, M – число серий опытов.

function p=var_01(M,N,n)

for k=1:M

sovp=0;

for i=1:N

dr=randint(n,1,[1 365]);

sdr=sort(dr);

if sum(diff(sdr)==0)>0

sovp=sovp+1;

end

end

p(k)=sovp/N;

hist(p,20)

end

Проделаем 1000 серий по 1000 опытов для 23 человек.

Получим следующую гистограмму:

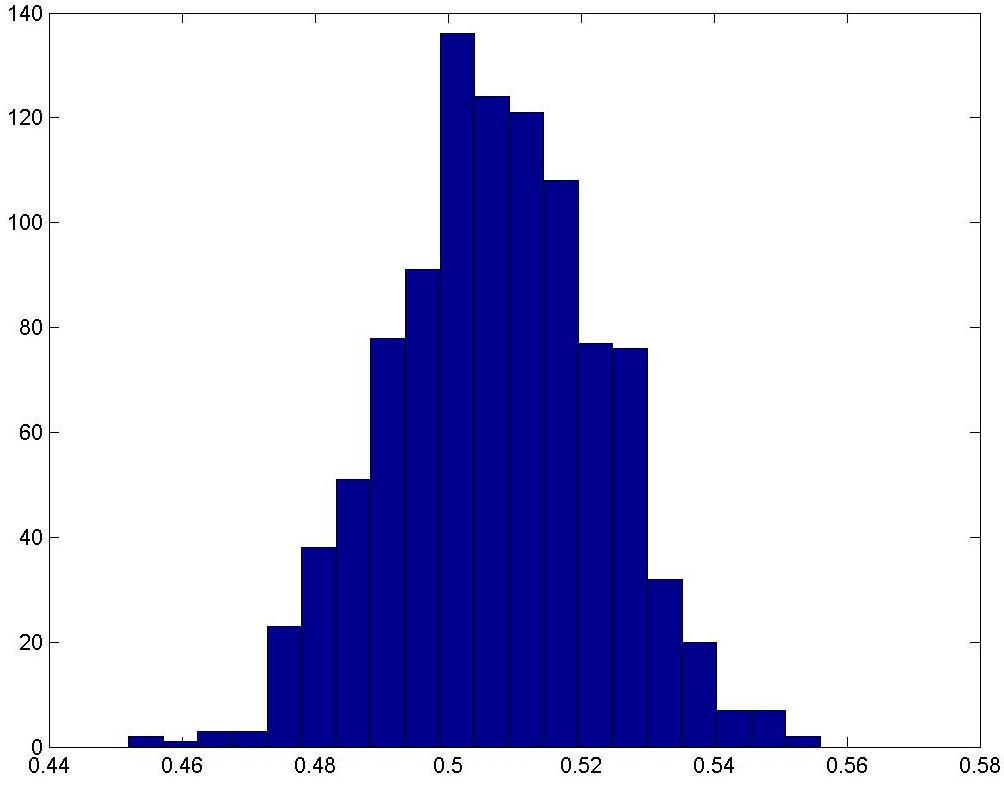
Проделаем 1000 серий по 1000 опытов для 77 человек.

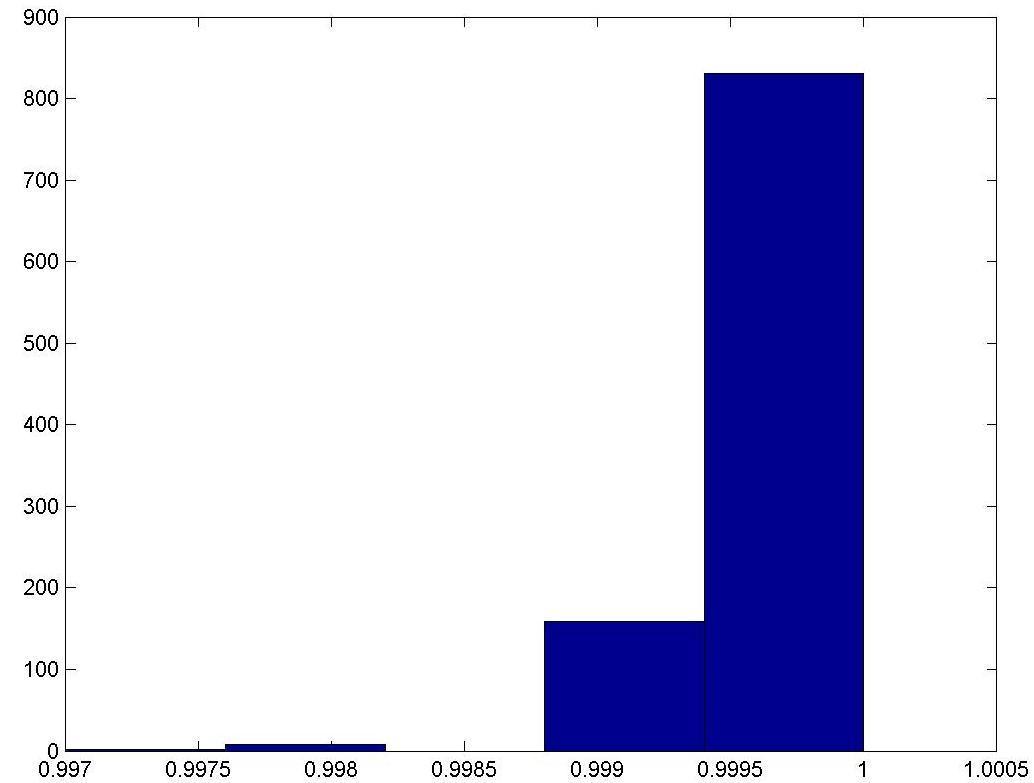
5. 2-й вариант эксперимента

Исследуем случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных. Ясно, что она может принимать значение от 1 до 55 (примерно).

Будем последовательно генерировать день рождения каждого нового опрошенного: a(1)=0;a(2)=floor(365*rand)+1; и т.д. a(i+1), до тех пор, пока день рождения вновь опрошенного не совпадет с днем рождения кого-либо из ранее опрошенных. Для этого будем использовать оператор while и параметр остановки цикла s, который первоначально будет равен нулю, а после совпадения дней рождения единице. Для того, чтобы выяснить совпали ли дни рождения, используем оператор сравнения if a(i+1)-a(k)==0 в цикле сравнения for k=1:i.

a(1)=0;

s=0;

i=1;

while s==0

a(i+1)=floor(365*rand)+1;

for k=1:i

if a(i+1)-a(k)==0;

s=1;

end

end

i=i+1;

end

k=i-1