1. Отчёт по лабораторной работе №3.

Объект исследования.

1. Задание 1.

Исследуем вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}. Здесь фиксированное число участников эксперимента - n и много серий экспериментов - N по n опросов каждая, в каждом опыте серии либо произойдет событие А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}, либо нет. Это даст Вам возможность вычислить частоты наступления события A для аудитории в n человек. Представьте результаты, выделив случай n=77 (как у нас на лекции) и n=23.

2. Задание 2.

Исследуем случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных.

Выполнение работы.

3. Математическая модель. Упрощения.

В задачах с помощью MATLAB мы строим «потоки» людей с различными датами дней рождений. Для облегчения расчетов и записи кода для MATLAB-а мы не учитываем дни, месяцы, а просто пишем номер дня в году (какой-то из 365). Так же мы не учитываем возможность рождения человека в високосный год, но все эти лишения не оказывают существенного вклада в результат эксперимента.

4. Пригодность генератора случайных чисел.

Проведём эксперимент: создадим массив из 100 000 чисел от 1 до 365. И посмотрим с помощью гистограммы, на разброс случайных выпадений.

mas=zeros(365);

for i=1:100000

temp=randint(1,1,[1 365]);

mas(temp)=mas(temp)+1;

end

hist(mas,365);

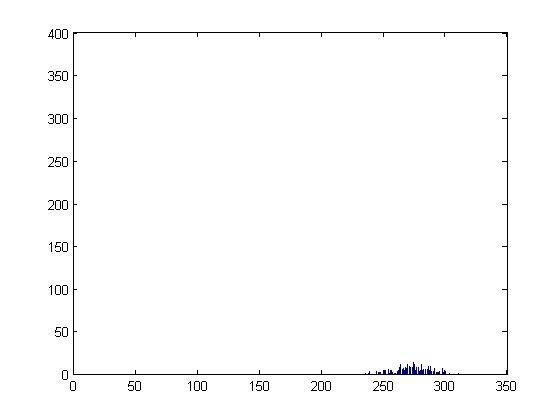
Как видно из графика, есть небольшие преобладания в выпадении некоторых чисел, но в целом такая ситуация вполне устраивает нас и мы можем проводить эксперимент.

5. Задание 1.

Смоделируем данную задачу, проведя 5000 экспериментов, есть ли среди n студентов повторяющиеся дни рождения или нет. И таких опытов сделаем 500 штук:

function dr(students);

main_test=500;

test=5000;

g=zeros(main_test,1);

main_like=0;

for j=1:main_test

for i=1:test

flag=0;

mas=randint(students,1,[1 365]);

like=zeros(365,1);

for k=1:students

if (like(mas(k))==0) like(mas(k))=1;

else flag=1;

end

if (flag==1) break;

end

end

if (flag==1) main_like = main_like+1;

flag=0;

end

end

g(j)=main_like/test*100;

main_like=0;

end

hist(g,50);

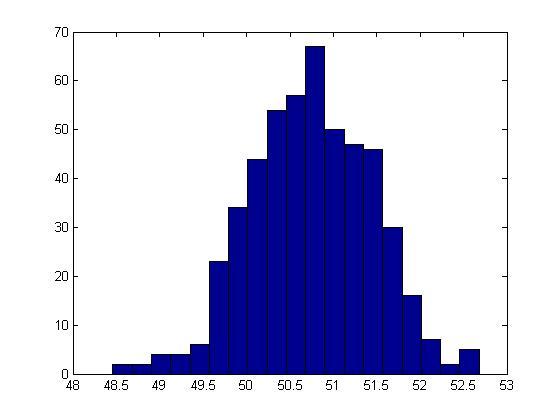
Результат для 23 человек:

Результат для 77 человек: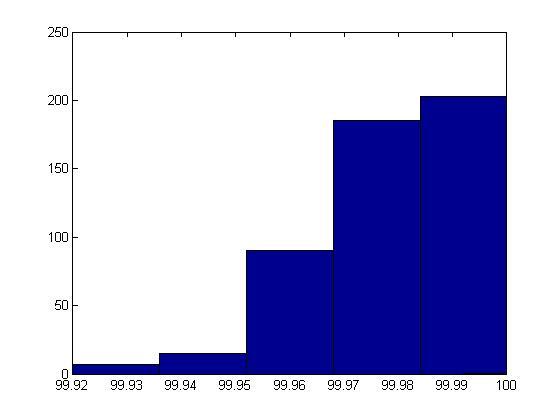

Как мы видим, вероятности совпадения дней рождений очень сильно зависят от того, сколько человек учавствует в эксперименте. Если их 23 – то вероятность совпадения, как говорят люди, пятьдесят на пятьдесят. Ну а уж если 77, то, судя по графику, мы можем со стопроцентной уверенностью говорить, что среди них есть повторяющиеся. Последний рисунок очень ярко это демонстрирует.

Посчитаем данную вероятность теортически. Для этого возьмем событие A={в группе из n человек хотя бы у двух совпадут дни рождения}. Этот расчет немного сложен, поэтому посчитаем вероятность невыполнения условия А ~А={ в группе из n человек ни у кого др не совпадет}. А результирующую вероятность найдем по формуле P(A)=1 – P(~A):

P(1)=1;

for i=2:23

P(i)=P(i-1)*(365-i)/365;

end

p=P(23)

В результате расчетов получим вероятность 49 процентов несовпадения, что означает, что вероятность совпадения равна 51 проценту, что в точности совпадает с экспериментом.

6. Задание 2

А теперь смоделируем следущую ситуацию – мы встанем на проходной института и у входящих студентов будем спрашивать даты их дней рождений. Как только встретим повторяющиеся, студента остановим и запишем номер, каким по счету прошел мимо нас этот студент. А дальше посчитаем вероятность Того или иного номера. Итак, Возьмем 500 000 учебных дней и будем заниматься нашим экспериментом:

test=500000;

f=zeros(test,1);

for i=1:test

number=0;

mas=randint(365,1,[1 365]);

find=zeros(365,1);

for k=1:365

if (find(mas(k))==0) find(mas(k))=1;

else number=k;

end

if (number~=0) break

end

end

f(i)=number;

end

hist(f,100);

Гистограмма

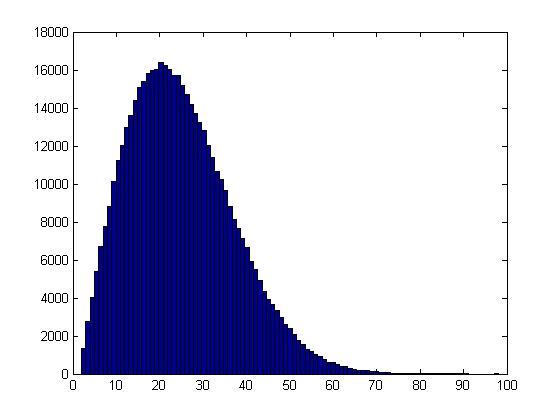
Наши правнуки через несколько тысячелетий может и получили бы данную гистограмму, не будь у них компьютера, а мы можем за несколько секунд выполнить данный код и насладиться результатом. Так вот, мы видим, что чаще всего попадаются совпадающие дни рождения примерно на 20 человеке, а вот дальше идет плавный спад и как мы видим, среди такого большого количества опытов больше 100 человек ни разу не насчитали.