Лабораторная работа № 3

1. Постановка задачи

Смоделировать эксперимент с совпадающими днями рождения. В первой части эксперимента необходимо исследовать вероятность наступления события А={хотя бы у двух участников эксперимента из m человек дни рождения совпадут}. Во второй части нужно исследовать случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных.

2. План эксперимента

   1. Анализ задачи

Объектом исследования являются аудитории, каждая из которых состоит из m (фиксированного числа) участников эксперимента. Чтобы построить математическую модель задачи, нужно сделать некоторые упрощающие предположения. В аудитории не должны находиться люди, у которых день рождения приходится на 29 февраля, иначе мы не будем иметь дело с равновероятными исходами.

2. Используемые средства

Команда randint представляет собой генератор случайных чисел, позволяющий смоделировать процесс, в котором у каждого участника эксперимента день рождения выбирается случайным образом и ни от чего не зависит. Случай с 29 февраля исключён.

3. Алгоритм

В первой части эксперимента необходимо провести N серий наблюдений по n опросов при фиксированном числе участников m. В каждом опыте серии либо произойдет событие А, либо нет.

Если у каких-то двух людей дни рождения совпадут, результатом данного опыта будет успех. В каждой серии вычисляется частота успехов, после этого на основе полученных данных можно построить гистограмму частот.

Во второй части эксперимента нужно провести N опытов, в каждом из которых последовательно опрашиваются участники и их дни рождения сравниваются с днями рождения всех ранее опрошенных. Как только обнаружится совпадение, опыт останавливается. Его результатом будет число X – номер человека, на котором прервался опрос. Заметим, что X не может быть больше 366, так как у 366-го человека день рождения точно совпадёт с кем-то из предыдущих людей, если до этого совпадений не было (29 февраля у нас по-прежнему нет).

3. Реализация в MATLAB

   1. Код программы 1

function P=dr1(m,n,N)

P=zeros(n,1);

for i=1:N

Result=zeros(n,1);

for j=1:n

dr=randint(m,1,[1 365]);

sdr_s=sum(diff(sort(dr))==0);

if sdr_s>0

Result(j)=1;

end

end

P(i)=sum(Result)/n;

end

2. Пояснения к программе 1

В каждом опыте после генерации массива случайных дней рождения происходит его сортировка, а затем вычисление разницы между соседними элементами. Если какие-то элементы совпадают, обязательно где-то возникнет разница, равная нулю. Число таких разниц и записывается в переменную sdr_s. Если оно оказалось больше нуля, опыт дал успех.

В конце каждой серии вычисляется частота успехов и записывается в массив P. После выполнения программы с помощью команды hist можно вывести на экран гистограмму частот.

3. Результаты первой части эксперимента

Случай n=23

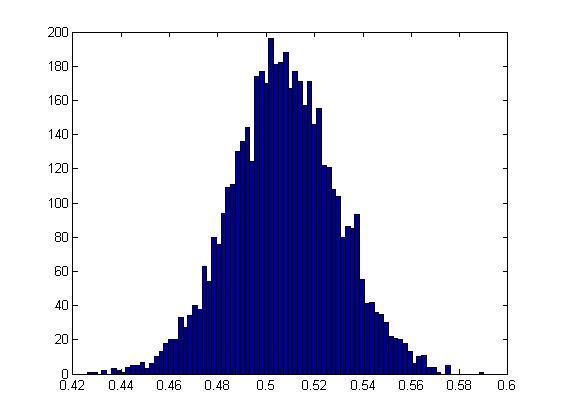
Случай n=77

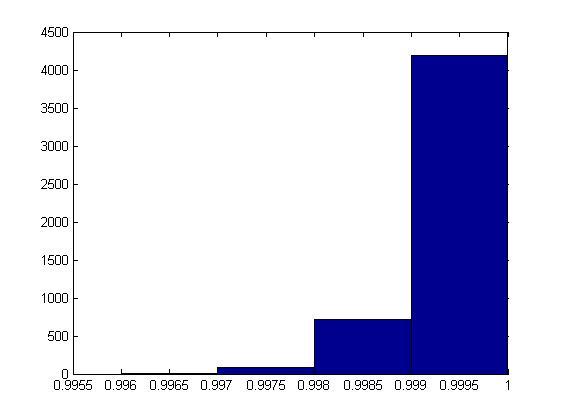
По оси абсцисс отложены диапазоны частот, по оси ординат – числа, показывающие, сколько серий в эксперименте удовлетворяют тому или иному диапазону.

4. Код программы 2

function x=dr2(N)

x=zeros(N,1);

for i=1:N

dr=zeros(366,1);

for j=1:366

dr(j)=randint(1,1,[1 365]);

B=0;

for k=1:j-1

if dr(j)==dr(k)

B=1;

break

end

end

if B==1

x(i)=j;

break

end

end

end

5. Пояснения к программе 2

В каждом опыте за одну итерацию цикла происходит генерация всего лишь одного дня рождения. Затем этот день рождения сравнивается с ранее полученными в данном опыте. Если обнаружено совпадение, в массив x будет записан номер последнего участника и опыт прекратится.

После выполнения программы с помощью команды hist можно вывести на экран гистограмму, показывающую распределение величины X.

6. Результаты второй части эксперимента

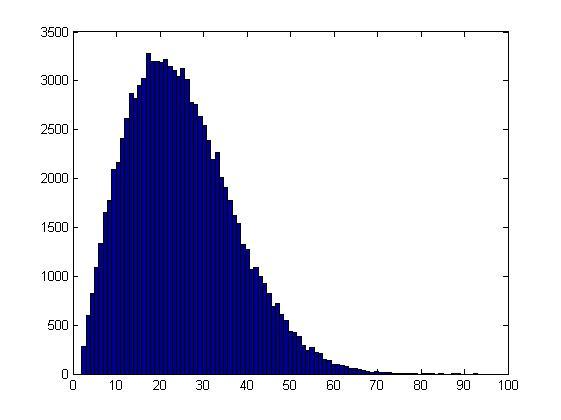
По оси абсцисс отложены значения случайной величины X, по оси ординат – числа, показывающие, сколько раз в эксперименте получилось данное значение X. В данном эксперименте N=100000.

4. Теоретические расчёты

Расчёт теоретического значения вероятности успеха в первой части эксперимента можно выполнить средствами MATLAB:

function P=theory(m)

P=1;

for i=2:m

P=P*((365-i+1)/365);

end

P=1-P;

Здесь сначала вычисляется вероятность противоположного события, то есть неуспеха. Для этого нужно, чтобы дни рождения у всех участников были различны. Тогда у первого участника есть 365 способов выбора дня рождения, у второго – уже на один меньше, у третьего – на два меньше и так далее. По формуле умножения вероятностей получим результат, представленный формулой в коде программы. Вероятностью интересующего нас события (успеха) будет единица без вероятности неуспеха.

При m=23 P=0,5073, при m=77 P=0,9998.

График распределения вероятностей во втором эксперименте можно получить с помощью следующего алгоритма:

function P=theory2()

x=1;

P(1)=0;

for i=2:366

x=x*((365-i+1)/365);

P(i)=x*((i-1)/365)*100000;

end

plot(P);

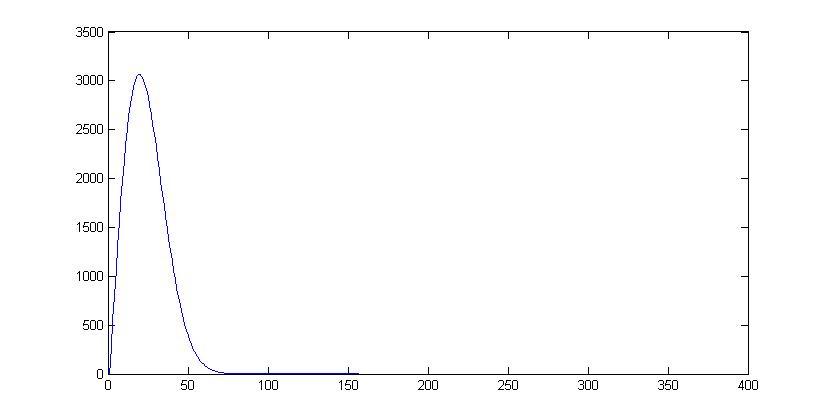
Вероятность появления искомой случайной величины определяется как произведение вероятностей несовпадения дней рождения у всех опрошенных участников, кроме последнего, и вероятности совпадения дней рождения у последнего участника и кого-то из ранее опрошенных. Мы умножили полученный результат на 100000, чтобы сравнить его с экспериментом, в котором было проведено 100000 опытов.

5. Выводы

В данной лабораторной работе исследовалось явление, называемое в литературе парадоксом дней рождения. Для кого-то оно может показаться удивительным, но на самом деле ничего тут странного нет, ведь проверяется не вероятность совпадения дней рождения с конкретным человеком в группе, а вероятность того, что совпадение произойдёт хотя бы у двух произвольных людей. Тем не менее, можно привести аномальный пример из своего личного опыта. В моей бывшей группе в институте (23 человека) и нынешней (18 человек) имеются люди (причём разные), у которых дни рождения совпали конкретно с моим. Нетрудно посчитать, что вероятность такой ситуации составляет около 0,3%. Но это было небольшое отступление.

Как видно из гистограмм, графика и полученных результатов, эксперимент подтверждает теорию. Когда число участников эксперимента равно 23, вероятность совпадения дней рождения по крайней мере у двух человек составляет около 50%. Когда же число участников равно 77, вероятность очень близка к единице, но не достигает её. Обратим внимание, что во втором исследовании (величины, равной номеру участника, на котором опыт прервался), максимум достигается при m=20, а не при m=23, как может показаться на первый взгляд. Это объясняется тем, что во втором эксперименте мы исследуем нечто другое: если в предыдущем случае мы могли получить совпадение при опросе любого человека с номером, меньшим либо равным m, то теперь мы получаем его только при опросе человека с номером m.