Лабораторные работы - Выполненые / Студенты всех групп / LAB_03 / МП-34 / 21_Kosenkov_03

• Отчёт по лабораторной работе №3.

• Задание.

Статистическое моделирование эксперимента с совпадающими днями рождения студентов. 1 Вариант. Исследуем вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}. 2 Вариант. Исследуем случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных.

• Выполнение работы. 1 задание.

• Объект исследования.

Исследуется вероятность совпадения дней рождений у ограниченного круга людей.

• Упрощающие предположения.

Мы предполагаем, что год не разбит на месяцы. Также мы предполагаем, что в году 365 дней.

• Эксперимент.

Выполнение эксперимента для первого задания с количеством человек в аудитории n=23:

Текст программы:

n=23;

dr=365;

op1=1000;

op2=10000;

mas=zeros(n);

bingo=zeros(op1);

for j=1:op1

for i=1:op2

mas=randint(n,1,[1 dr]);

sortm=sort(mas);

sortm_mas=diff(sortm);

if sum(sortm_mas==0)>0

bingo(j)=bingo(j)+1;

end

end

b(j)=bingo(j)/op2;

end

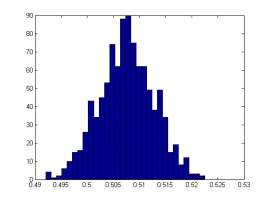hist(b,30)

Результат выполнения:

Выполнение эксперимента для первого задания с количеством человек в аудитории n=77:

Текст программы:

n=77;

dr=365;

op1=1000;

op2=10000;

mas=zeros(n);

bingo=zeros(op1);

for j=1:op1

for i=1:op2

mas=randint(n,1,[1 dr]);

sortm=sort(mas);

sortm_mas=diff(sortm);

if sum(sortm_mas==0)>0

bingo(j)=bingo(j)+1;

end

end

b(j)=bingo(j)/op2;

end

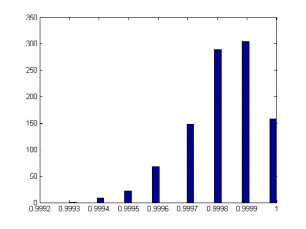hist(b,30)

Результат выполнения:

• Задание 2.

• Объект исследования.

Мы стоим в людном месте и спрашиваем у людей их дни рождения. Эксперимент заканчивается, когда находится человек, чей день рождения совпал днём рождения кого-либо раньше. Порядковый номер этого человека записывается, эксперимент проводится много раз. Упрощающие предположения те же, что и в первом задании.

• Эксперимент.

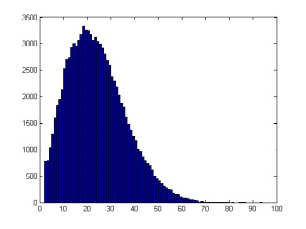
Код программы:

dr=365;

op1=100000;

mas=zeros(dr+1,1);

f=zeros(1,1);

flgs=zeros(op1,1);

for j=1:op1

f=0;

bin=zeros(dr+1,1);

mas=randint(dr+1,1,[1 dr]);

for i=1:dr+1

if bin(mas(i))==0

bin(mas(i))=1;

else

f=i;

end

if f~=0

break;

end

end

flgs(j,1)=f;

end

hist(flgs,87)

Результат эксперимента:

• Вывод:

Результаты 1 эксперимента совпали с теоретическими значениями вероятностей. Математическая модель данного эксперимента имеет право на существование. Теория: событие А={в группе из n=23 человек хотя бы у двух совпадут д.р.}. Берём обратное событие ~А. Р(А)=1-Р(~А). Найдём Р(~А):

P(1)=1;

for i=2:23

P(i)=P(i-1)*(366-i)/365;

end

p=P(23)

Имеем p=49%, откуда р(А)=51%.