Лабораторная работа № 3

Статистическое моделирование лекционного эксперимента с совпадающими днями рождения студентов групп МП-30, МП-34, МП-35, присутствовавших на лекции 3.09.2009 г.

1. Объект исследования

Объектом исследования является совпадение дней рождения в группе учащихся.

2. Идеализация объекта

• Дни рождения учащихся определяются случайным образом (ГСЧ).

• В году всегда 365 дней.

3. Эксперимент

   1. Вариант 1

      1. Исследуем вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}.

      2. Программа

n = 30;

N = 100;

m = 0;

k=0;

for i=1:N

dr = sort(floor(365*rand(n,1)+1));

k = 0;

for j=2:n

if dr(j)-dr(j-1) == 0

k = k + 1;

end

end

if k>0

m = m + 1;

end

end

P = m / N

1. Результаты эксперимента

• n = 10

N = 100

P = 0.11

• n = 10

N = 1000

P = 0.102

• n = 30

N = 100

P = 0.73

• n = 50

N = 100

P = 0.94

• n = 100

N = 1000

P = 1

При увеличении N повышается точность определения вероятности.

• n = 77

N = 100

P = 1

• n = 77

N = 10000

P = 0.9997

• n = 23

N = 100

P = 0.56

Получаем при n = 77 практически 100% вероятность совпадения дней рождения.

1. Решение задачи: совпадение дней рождения у 3 человек.

• n = 23

N = 100

P = 0.015

• n = 77

N = 1000

P = 0.376

• n = 200

N = 10000

P = 0.9994

2. Вариант 2

   1. Исследуем случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных.

   2. Программа

N = 10000;

n = 10;

XX = zeros(1, n);

for h=1:N;

dr = floor(365*rand(n,1)+1);

for i=1:n-1

k = 0;

for j=i+1:n

if dr(j)-dr(i) == 0

k = j;

break;

end

end

if k>0

break;

end

end

if k > 0

XX(h) = k;

end

end

XX

hist(XX,1:1:n)

NN=hist(XX,1:1:n)

NN(1) = 0;

NNS=cumsum(NN)

plot(NNS)

3. Результаты экспериментов

0 – Совпадений не было

• N = 10000;

n = 77;

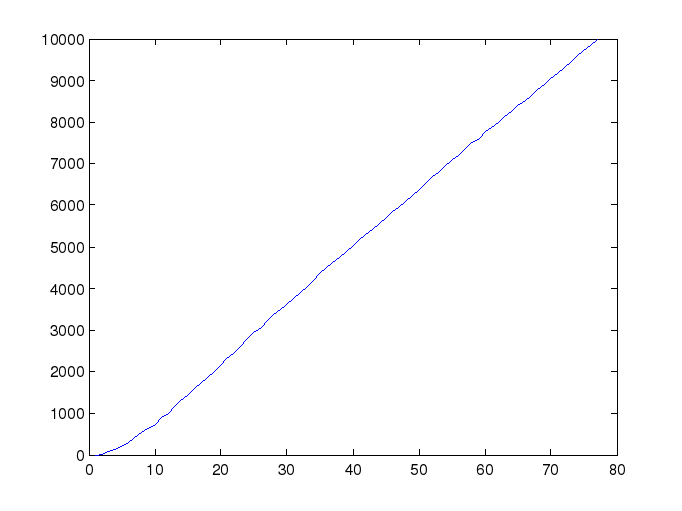
Из графика можно определить, что примерно в 50% повторах к 40 номеру ученика найдутся ученики с одинаковыми днями рождения.

• N = 10000;

n = 10;

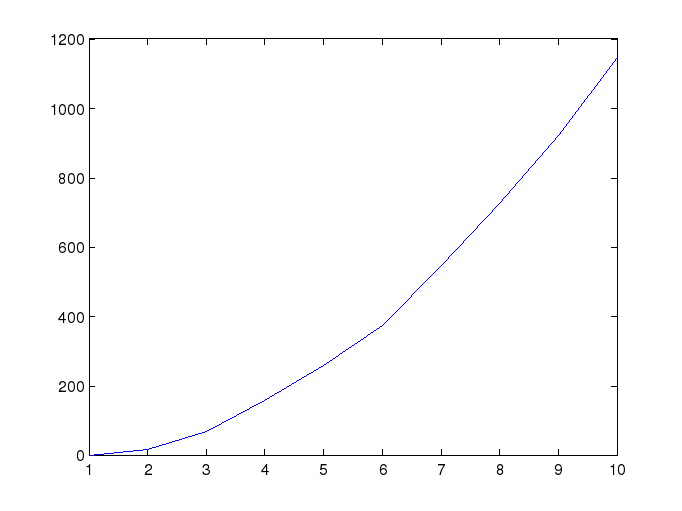
Из этого графика видно, что даже при прохождении всех итераций, количество совпадений дней рождения не совпадает с количеством повторов. Это можно объяснить тем, что для 10 человек вероятность совпадения дней рождения меньше 100% (а точнее около 10%).

4. Заключение

В первом варианте эксперимента мы исследуем вероятность совпадения дней рождения у хотя бы двух учеников, а во втором вероятность наступления этого события к конкретному номеру ученика.

То есть, если взять рассмотренный пример с 77 учениками, с вероятностью 50% к 40 ученику совпадение дней рождения произойдёт. С вероятностью 90% к 70 ученику.