Лабораторная работа №3

Статистическое моделирование лекционного эксперимента с совпадающими днями рождения студентов групп МП-30, МП-34, МП-35

Выполнение работы:

1. Объект исследования

Объектом исследования является вероятность выпадения двух совпадающих чисел из 365 в зависимости от числа экспериментов. В нашем случае мы рассматриваем дни рождения и число экспериментов, это, по сути, число участвующих человек.

2. Упрощающие предположения

Для построения математической модели предполагаем, что дата дней рождения является случайными числом от 1 до 365, все даты равновероятны. Данное упрощение применимо, т.к. случайным образом происходит отбор людей.

3. Варианты исследований

   1. Исследование №1.1

А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}

Всего N экспериментов.

Содержимое m-файла:

N=20;

u=1;

for n=10:80

for k=1:N

Mas=floor(rand(1,n)*365+1);

i=0;

d=1;

rez=0;

while d==1

c=1;

i=i+1;

j=i;

while c==1

j=j+1;

if Mas(i)==Mas(j)

c=0;

d=0;

rez=Mas(j);

end

if j==n

c=0;

end

end

if i==(n-1)

d=0;

end

end

O(k)=rez

end

O

s=sum(O==0);

S=N-s;

A(u)=S/N

u=u+1;

end

plot (A)

Данный график показывает зависимость вероятности совпадения от количества человек (n) в 20-ти экспериментах.

При различных n будет различное значение статистической частоты встречаемости. Причем при n=23 она переходит за 50%. С увеличением числа опытов N, уменьшается отклонение значения статистической частоты от теоретической вероятности.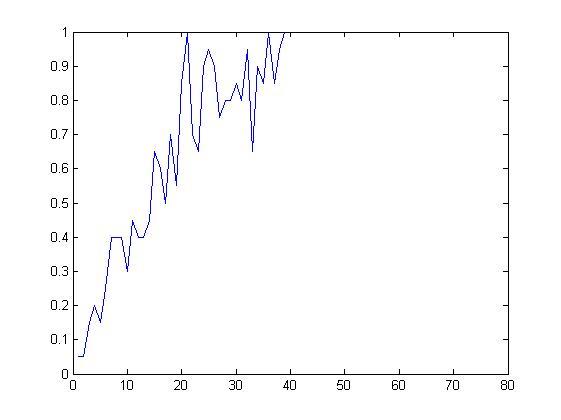

При n=23 статистическая частота около 50%, при 77 - около 99,9% .

2. Исследование №1.2

Теперь попробуем теоретически решить задачу «С какой вероятностью дни рождения совпадут у 3 участников»,

Вероятность совпадения дней рождения в группе можно также рассчитать с использованием формул комбинаторики. Представим, что каждый день года — это одна буква в алфавите из 365 букв. Дни рождения n человек могут быть представлены строкой, состоящей из n букв такого алфавита. Общее число таких строк равно

n(общ)=365^n

Общее число строк, в которых буквы не повторяются, составит

n(неповт)=365!/(365-n)!

Тогда, если строки выбираются случайно (с равномерным распределением), то вероятность выбрать строку, в которой хотя бы две буквы совпадут, равна

p(n)=1-n(неповт)/n(общ)

Теперь определим вероятность того, что дни рождения совпадут у 3 участников:

p(n)=1-n(неповт)- 1+n(неповт)/n(общ)=-n(неповт)+n(неповт)/n(общ).

3. Исследование №2

Теперь рассматриваемым объектом будет номер человека, на котором произошло совпадение дат.

Проделаем 10000 экспериментов:

p=zeros(10000,1);

for k=1:10000

flag=0;

dr=zeros(166,1);

dr(1)=randint(1,1,[1 365]);

for i=2:366

dr(i)=randint(1,1,[1 365]);

for j=1:(i-1)

if dr(i)==dr(j) flag=1;

end

end

if flag==1 break;

end

end

p(k)=i;

end

hist(p)

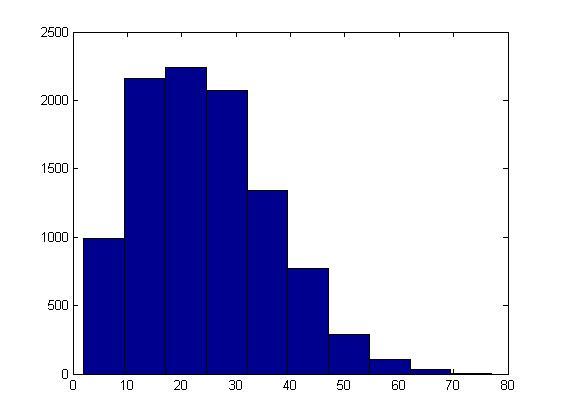
По гистограмме видно, что большинство совпадений приходится на второй десяток человек, несколько реже происходят совпадения у людей с номером больше 30, и еще реже у людей с номером меньшим 20. Полученные результаты вполне соответствуют проделанному ранее эксперименту, там, когда число участников доходит до 20 вероятность совпадения дат возрастает до 50%!