Лабораторная работа №3

Статистическое моделирование лекционного эксперимента с совпадающими днями рождения.

1. Постановка задачи

   1. Вариант 1

Исследовать вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}. Здесь фиксированное число участников эксперимента.

2. Вариант 2

Исследовать случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных.

2. Моделирование Эксперимента

   1. Объект исследования

Объектом исследования является эксперимент с совпадающими днями рождения.

2. Упрощающие предположения

Для того чтобы построить математическую модель эксперимента мы должны ее упростить, а именно предположить, что дни рождения распределены равновероятно в году.

3. Генератор случайных чисел

День рождения мы будем задавать при помощи генератора случайных чисел. Теперь нам нужно проверить, что дни рождения равновероятно распределены в году. Для этого создадим массив из 10000 элементов и построим гистограмму

Вот какую гистограмму нарисовал нам Matlab

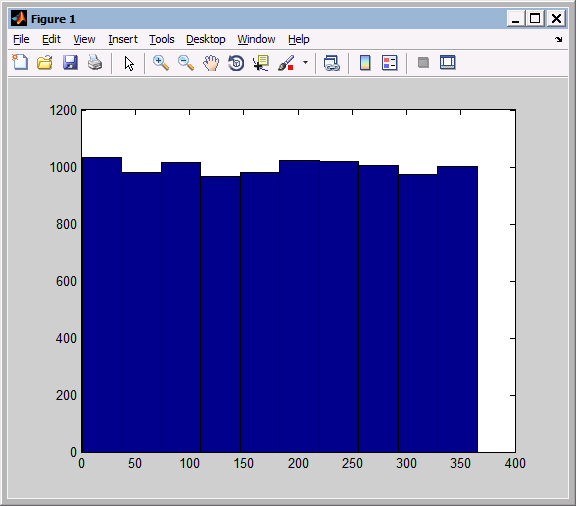
3. Эксперимент 1

   1. Математическая модель

Создадим массив размером 1xn, заполним его случайными числами. Затем создадим результирующий массив 1xN, каждый элемент которого будет равен 1 если в предыдущем массиве было хоть одно совпадение дней рождений и 0 если не было. Таким образом, мы смоделируем N серий экспериментов - по n опросов каждая.

2. Частотная характеристика

При помощи Matlab получим частотные гистограммы, из которых наглядно, видно процент совпадений дней рождений

1. Для n=45;N=1000

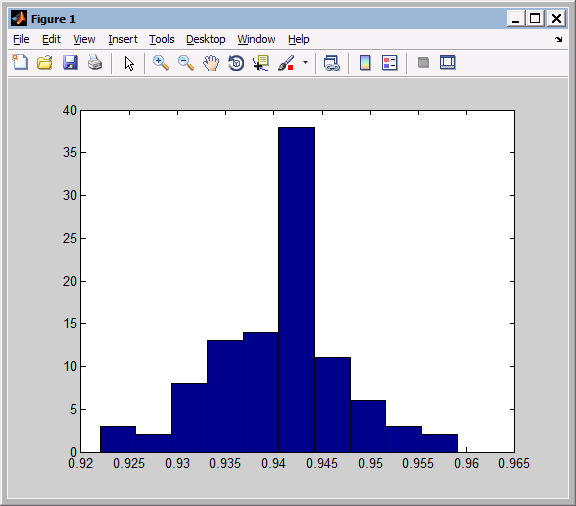
2. Для n=23;N=1000

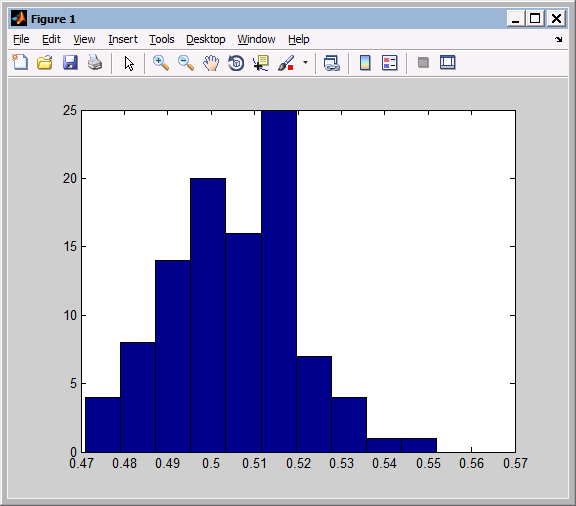
4. Эксперимент 2

   1. Математическая модель

Смоделируем данный эксперимент, последовательно заполняя массив 1xN, где N – количество проведенных экспериментов. Элементами этого массива будут случайные величины Х - номера опрошенных участников, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных.

2. Частотные характеристики

При помощи Matlab получим частотные гистограммы, из которых наглядно, видно величину X и количество ее повторений в смоделированных экспериментах

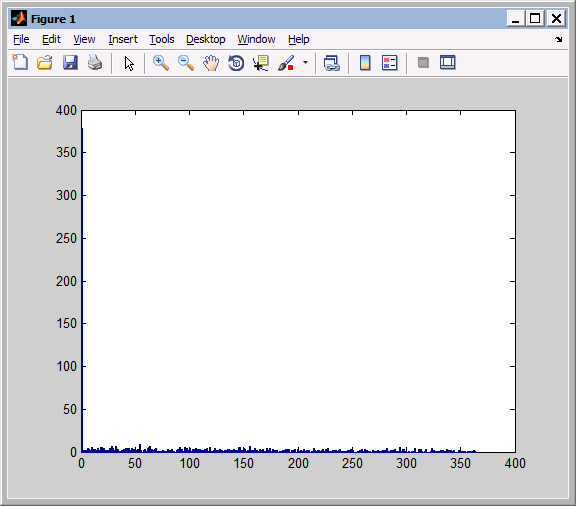
5. Приложение

   1. Код функции

      1. Эксперимент 1

function res=var_1(N,n)

res=zeros(1,N);

for i=1:N

x=randi(365,1,n);

difer=sum(diff(sort(x))==0);

if (difer>0)

res(:,i)=1;

end

hist(res,0:1)

end

>> for k=1:100,U(k)=sum(var_1(1000,23))/1000;end

>> hist(U)

2. Эксперимент 2

function y=var_2(N)

y=zeros(1,N);

x=zeros(1,366);

for j=1:N

flag=0;

for i=1:365

a=randi(365,1,1);

for k=1:366

if (x(:,k)==a) flag=i; break;

end

end

x(:,k)=a;

if (flag>0) y(:,j)=flag; break;

end;

end

end