Лабораторная работа № 3

Оглавление

1. Статистическое моделирование лекционного эксперимента с совпадающими днями рождения студентов 2

Постановка задачи 2

Подготовьте ответы на следующие вопросы 2

Что является объектом исследования? 2

Какие упрощающие предположения Вы делаете, чтобы построить математическую модель объекта? 2

Реализация экспериментов 2

Вариант I 2

Вариант II 7

1. Статистическое моделирование лекционного эксперимента с совпадающими днями рождения студентов

Постановка задачи

Смоделируйте подобный эксперимент В MATLAB и исследуйте полученные результаты.

Подготовьте ответы на вопросы.

Подготовьте ответы на следующие вопросы

Что является объектом исследования?

Объектом исследования являются группа студентов в лекционном зале.

Какие упрощающие предположения Вы делаете, чтобы построить математическую модель объекта?

Для упрощения постановки задачи мы берем 365 дней в году.

Нам надо реализовать два варианта эксперимента.

Реализация экспериментов

Вариант I

Исследуем вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}. Здесь фиксированное число участников эксперимента - n и много серий экспериментов - N по n опросов каждая, в каждом опыте серии либо произойдет событие А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}, либо нет. Это даст Вам возможность вычислить частоты наступления события A для аудитории в n человек.

Вспомните статистическое определение вероятности.

Составьте блок-схему алгоритма реализации математической модели эксперимента и предъявите преподавателю.

>> dr=randint(45,1,[1 365]);

>> dr

dr =

52

154

335

290

351

240

14

310

341

248

277

272

144

240

63

258

12

102

17

36

301

254

116

347

13

161

140

280

291

69

179

163

236

259

276

101

249

240

60

44

182

351

125

214

82

>> sdr=sort(dr);

>> sdr

sdr =

12

13

14

17

36

44

52

60

63

69

82

101

102

116

125

140

144

154

161

163

179

182

214

236

240

240

240

248

249

254

258

259

272

276

277

280

290

291

301

310

335

341

347

351

351

>> sdr_s=diff(sdr)

sdr_s =

1

1

3

19

8

8

8

3

6

13

19

1

14

9

15

4

10

7

2

16

3

32

22

4

0

0

8

1

5

4

1

13

4

1

3

10

1

10

9

25

6

6

4

0

>> sum(sdr_s==0)

ans =

3

>>

Создайте m-файл(ы) с программами экспериментов (например: var_01.m и др.).

Создал файл dr.m для генерации дней рождений у N человек.

function a=dr(N)

% генерация дней рождений

a = randint(N,1,[1 365])

a(1)=0;

p=0;

i=1;

while p==0

a(i+1)=floor(365*rand)+1;

for k=1:i

if a(i+1)-a(k)==0;

p=1;

end

end

i=i+1;

end

k=i-1;

Еще для простоты провидения анализа, создали еще один m-файл который выводит число повторений чисел в массиве.

function b=sumdr(K)

% подсчет совпадающих чисел

sdr=sort(K);

sdr_s=diff(sdr);

b = sum(sdr_s==0);

Что можно сказать о вероятностях наступления события А для различных n? Исследуйте влияние числа N.

>> A = dr(10)

A =

0

195

365

330

6

285

178

143

301

320

365

>> sumdr(A)

ans =

1

>> A = dr(100);

>> sumdr(A)

ans =

14

>> A = dr(1000);

>> sumdr(A)

ans =

655

>> A = dr(10000);

>> sumdr(A)

ans =

9634

>>

Представьте результаты преподавателю, выделите случай n=77 (как у нас на лекции) и n=23. Вы уже можете сообщить нам теоретическое решение этой задачи! Сравните результаты моделирования и точное (в рамках модели) решение.

Попробуйте смоделировать и теоретически решить задачу для более сложного события {совпадение дней рождения хотя бы у трех присутствующих в аудитории} (как это имело место у нас на лекции). Ваши комментарии.

Вариант II

Исследуем случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных. Ясно, что она может принимать значения от 1 до (чего?). Поэтому надо использовать или оператор while (см. help while) или оператора for (см. help for) (до чего?) с выходом из цикла по условию (см. help break).

Составьте блок-схему алгоритма реализации математической модели этого эксперимента и предъявите преподавателю.

Создайте m-файл(ы) с программами экспериментов (например: var_02.m и др.).

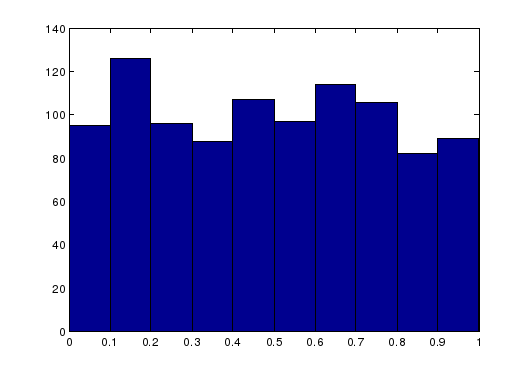
Полученную выборку XX (выборки), полученную для большого числа повторяющихся экспериментов изучаем с помощью гистограммы (help hist). Особо обратите внимание на возможность изменения числа интервалов разбиения hist(XX,15) по умолчанию их 10, задания вектора центров интервалов разбиения, получения чисел попадания в интервалы разбиения с заданными центрами NN=hist(XX,5:10:95). Последняя возможность позволяет построить накопленную гистограмму NNS=cumsum(NN); plot(NNS), что позволяет оценить функцию распределения этой случайной величины и оценивать вероятности попадания случайной величины Х в интересующий Вас интервал(ы).

Создайте файл отчета с результатами, опишите свои открытия и выводы. Как соотносятся эти два варианта исследований?

>> x=rand(1000,1);

>> hist(x)

>>

8