Лабораторная работа №3

1. Статистическое моделирование лекционного эксперимента с совпадающими днями рождения студентов групп МП-30, МП-34, МП-35, присутствовавших на лекции 3.09.2009

2. Что является объектом исследования?

Объектом исследования является вероятность совпадения двух дат с днями рождения у определенного количества человек, 77 и 23.

3. Какие упрощающие предположения Вы делаете, чтобы построить математическую модель объекта?

Год не разбивается по месяцам и датам, задается лишь номер дня, одного из 365. Так же в модель не входит понятия високосного дня, количество дней в году остается константой.

4. Эксперимент №1

Исследуем вероятность наступления события А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}. Здесь фиксированное число участников эксперимента - n и много серий экспериментов - N по n опросов каждая, в каждом опыте серии либо произойдет событие А={хотя бы у двух участников эксперимента из n человек дни рождения совпадут}, либо нет. Это даст Вам возможность вычислить частоты наступления события A для аудитории в n человек.

Теоретическое обоснование:

P(1)=1;

for i=2:23

P(i)=P(i-1)*(366-i)/365

end

p=p(23)

Получили вероятность примерно 51%. Проверим это на практике.

Смоделируем условие задачи.

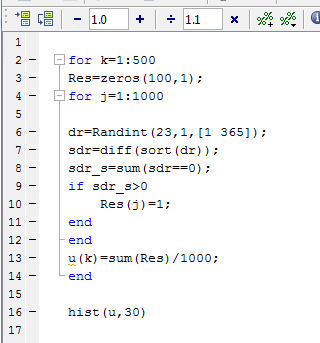
Получили следующую гистограмму.

Из нее что число 23 является граничным, появление совпадение при этом количестве 50% и большее количество участников эксперимента увеличит эту вероятность.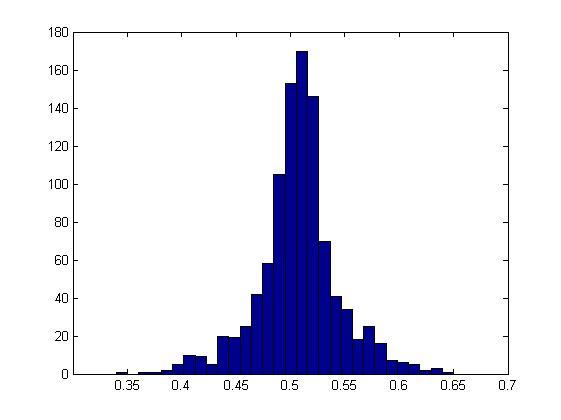

Увеличив количество человек до 77 получаем практически 100% вероятность

5. Эксперимент №2

Исследуем случайную величину Х - номер опрошенного участника, чей день рождения совпал с днем рождения кого-либо из ранее опрошенных. Ясно, что она может принимать значения от 1 до 365. Поэтому надо использовать или оператор while или оператора for, с выходом из цикла по условию.

Смоделируем условие задачи.

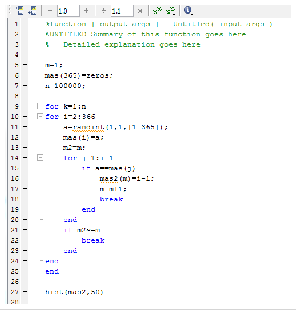
Получили следующую гистограмму: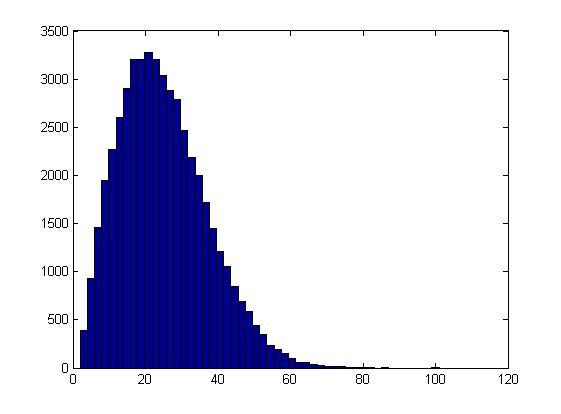

Из нее видно что максимальную вероятность наступления события получается при опросе 22-23 участников.

6. Вывод.

Результаты двух экспериментов получают одинаковое пороговое значение количества участников опроса - 23. При этом значении вероятность получить первое совпадение максимально.