
- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
19. Ординальные числа и их свойства.
Определение.
Порядковым
типом
вполне упорядоченного множества
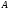 называется совокупность всех вполне
упорядоченных множеств, изоморфных
множеству
называется совокупность всех вполне
упорядоченных множеств, изоморфных
множеству
Порядковый
тип вполне упорядоченного множества
называется ординальным
(или порядковым)
числом
или просто ординалом.
Ординальные числа, соответствующие
конечным вполне упорядоченным множествам,
обозначаются 0, 1, 2, ... (их можно отождествить
с натуральными числами). Например, 3 –
это порядковый тип, соответствующий
трёхэлементной цепи
 (очевидно, все трёхэлементные цепи
изоморфны между собой). Наименьшее
бесконечное ординальное число – это
порядковый тип множестваN
натуральных чисел. Оно обозначается
символом
(очевидно, все трёхэлементные цепи
изоморфны между собой). Наименьшее
бесконечное ординальное число – это
порядковый тип множестваN
натуральных чисел. Оно обозначается
символом

Введём
отношение порядка среди ординалов.
Пусть
 – ординалы, а
– ординалы, а – соответствующие им вполне упорядоченные
множества. В предыдущем разделе было
доказано, что либо множество
– соответствующие им вполне упорядоченные
множества. В предыдущем разделе было
доказано, что либо множество изоморфно начальному отрезку множества
изоморфно начальному отрезку множества либо наоборот. Если множество
либо наоборот. Если множество изоморфно начальному отрезку множества
изоморфно начальному отрезку множества то считаем
то считаем
Докажем следующие свойства ординалов:
(1)
 (2)
(2)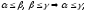 (3)
(3)
Доказательство.
Свойство (1) очевидно. Пусть теперь
 и
и Тогда существуютизотонные
(т.е. сохраняющие порядок) вложения
Тогда существуютизотонные
(т.е. сохраняющие порядок) вложения
 и
и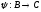 такие, что
такие, что – начальный отрезок в
– начальный отрезок в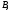 а
а – начальный отрезок в
– начальный отрезок в Произведение
Произведение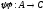 является изотонным вложением
является изотонным вложением в
в а
а – начальный отрезок множества
– начальный отрезок множества Значит,
Значит, т.е. выполнено (2). Осталось доказать
свойство (3). Пусть
т.е. выполнено (2). Осталось доказать
свойство (3). Пусть и
и – изотонные вложения, причём
– изотонные вложения, причём – начальный отрезок в
– начальный отрезок в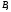 а
а – начальный отрезок в
– начальный отрезок в Произведение
Произведение является изотонным вложением. По
следствию из леммы предыдущего раздела
получаем, что
является изотонным вложением. По
следствию из леммы предыдущего раздела
получаем, что – тождественное отображение. Аналогично
доказывается, что
– тождественное отображение. Аналогично
доказывается, что – тождественное отображение. Значит,
– тождественное отображение. Значит,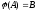 и
и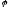 – изоморфизм, поэтому
– изоморфизм, поэтому
Как
обычно, мы считаем, что
 если
если и
и Например,
Например,

 Понятно, что из
Понятно, что из
 следует
следует
Введём теперь операцию сложения двух ординалов.
Определение.
Пусть
 и
и – ординалы, а
– ординалы, а и
и – соответствующие им вполне упорядоченные
множества. Будем считать, что
– соответствующие им вполне упорядоченные
множества. Будем считать, что Введём на множестве
Введём на множестве порядок, полагая, что на
порядок, полагая, что на и
и порядок прежний и, кроме того,
порядок прежний и, кроме того, при
при
 Ясно, что
Ясно, что вполне упорядочено. Его порядковый тип
называетсясуммой
вполне упорядочено. Его порядковый тип
называетсясуммой

Легко
видеть, что


 (множество
(множество имеет максимальный элемент, а
имеет максимальный элемент, а не имеет. Таким образом,
не имеет. Таким образом, в общем случае.
в общем случае.
Закон
ассоциативности
 имеет место для любых ординалов. Для
доказательства рассмотрим вполне
упорядоченные множества
имеет место для любых ординалов. Для
доказательства рассмотрим вполне
упорядоченные множества соответствующие ординалам
соответствующие ординалам Будем считать, что они попарно не
пересекаются. Тогда множество
Будем считать, что они попарно не
пересекаются. Тогда множество (где
(где при
при

 соответстует как числу
соответстует как числу так и числу
так и числу Значит,
Значит,
Определение.
Пусть
 – ординалы, соответствующие вполне
упорядоченным множествам
– ординалы, соответствующие вполне
упорядоченным множествам Произведением
Произведением
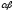 называется порядковый тип лексикографического
произведения
называется порядковый тип лексикографического
произведения (напомним, что
(напомним, что если либо
если либо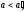 либо
либо
Нетрудно
видеть, что

 Следовательно,
Следовательно, в общем случае. Однако, ассоциативность
в общем случае. Однако, ассоциативность имеет место для любых ординалов – это
следует из легко проверяемого изоморфизма
имеет место для любых ординалов – это
следует из легко проверяемого изоморфизма Важное свойство ординалов даёт следующая
теорема.
Важное свойство ординалов даёт следующая
теорема.
Теорема 1. В любом множестве ординалов есть наименьший элемент.
Доказательство.
Пусть
 – множество ординалов. Обозначим через
– множество ординалов. Обозначим через вполне упорядоченное множество,
соответствующее ординалу
вполне упорядоченное множество,
соответствующее ординалу Возьмём какое-либо
Возьмём какое-либо и удалим из рассмотрения все
и удалим из рассмотрения все которые не изоморфны начальным отрезкам
множества
которые не изоморфны начальным отрезкам
множества Будем отождествлять множество
Будем отождествлять множество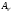 с его изоморфным образом, т.е. считать,
что
с его изоморфным образом, т.е. считать,
что – начальный отрезок
– начальный отрезок Для каждого
Для каждого такого, что
такого, что положим
положим Затем выберем наименьший элемент из
этих
Затем выберем наименьший элемент из
этих
 Легко видеть, что
Легко видеть, что – наименьший ординал в множестве
– наименьший ординал в множестве
Определение.
Ординал
 называетсяпредельным,
если соответствующее ему вполне
упорядоченное множество не имеет
наибольшего элемента, и непредельным,
если это не так.
называетсяпредельным,
если соответствующее ему вполне
упорядоченное множество не имеет
наибольшего элемента, и непредельным,
если это не так.
Например,
1, 2,

 – непредельные ординалы, а
– непредельные ординалы, а

 – предельные. Каково бы ни было ординальное
число
– предельные. Каково бы ни было ординальное
число существует число, непосредственно
следующее за ним – это число
существует число, непосредственно
следующее за ним – это число Нетрудно проверить, что ординал
Нетрудно проверить, что ординал является предельным в том и только том
случае, если он не имеет непосредственно
предшествующего, т.е. не представим в
виде
является предельным в том и только том
случае, если он не имеет непосредственно
предшествующего, т.е. не представим в
виде где
где – некоторый другой ординал.
– некоторый другой ординал.
Теорема
3. Каково бы
ни было множество ординалов
 существует ординал
существует ординал такой, что
такой, что при всех
при всех
Доказательство.
Рассмотрим вполне упорядоченные
множества
 соответствующие ординалам
соответствующие ординалам Пусть
Пусть и
и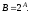 Тогда
Тогда при всех
при всех Следовательно, порядковый тип
Следовательно, порядковый тип множества
множества (вполне упорядоченное каким-нибудь
отношением порядка) больше всех
(вполне упорядоченное каким-нибудь
отношением порядка) больше всех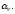
Замечание.
Если в теореме 3 мы возьмём “множество
всех ординалов”, то получим странное
утверждение: ординал
 больше любого ординала вообще, а значит,
больше самого себя:
больше любого ординала вообще, а значит,
больше самого себя: что невозможно. Борьба с эти противоречием
осуществляется следующим образом:все
ординалы не образуют множества.
Итак, мы запрещаем такие “множества”,
как “множество всех множеств”, “множество
всех ординалов”, “множество всех
линейных пространств” и т.д.
что невозможно. Борьба с эти противоречием
осуществляется следующим образом:все
ординалы не образуют множества.
Итак, мы запрещаем такие “множества”,
как “множество всех множеств”, “множество
всех ординалов”, “множество всех
линейных пространств” и т.д.
