
- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
15. Эквиваленстность множеств(см.Ниже)
Пусть
 – произвольные множества. Обозначим
через
– произвольные множества. Обозначим
через множество всех отображений
множество всех отображений
Теорема
3. Для любых
множеств
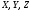 имеет место эквивалентность
имеет место эквивалентность

Доказательство.
Пусть

 Тогда
Тогда Для каждого
Для каждого пусть
пусть определено правилом
определено правилом По определению
По определению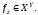 Значит, мы имеем отображение
Значит, мы имеем отображение
 Ясно, что
Ясно, что Положим
Положим Мы получили отображение
Мы получили отображение
Докажем,
что Ф является вложением. Действительно,
пусть
 Тогда
Тогда при некоторых
при некоторых
 Отсюда
Отсюда Значит,
Значит,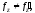 а потому
а потому Таким образом,
Таким образом, т.е.
т.е.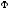 – вложение.
– вложение.
Осталось
доказать, что
 является наложением, т.е. что для каждого
является наложением, т.е. что для каждого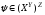 существует такое
существует такое что
что Имеем:
Имеем: Значит,
Значит, т.е.
т.е. Таким образом,
Таким образом, Положим
Положим Тогда
Тогда Осталось проверить, что
Осталось проверить, что Мы имеем:
Мы имеем: Ввиду произвольности элемента
Ввиду произвольности элемента получаем:
получаем: По определению
По определению Значит,
Значит,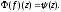 Ввиду произвольности элемента
Ввиду произвольности элемента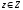 получаем:
получаем: Это и требовалось доказать.
Это и требовалось доказать.
Множество
всех отображений множества
 в двухэлементное множество
в двухэлементное множество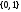 обозначим через
обозначим через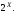
16. Вполне упорядоченные множества и их свойства.
Множество
 называетсявполне
упорядоченным,
если оно линейно упорядочено и любое
непустое его подмножество имеет
наименьший элемент.
называетсявполне
упорядоченным,
если оно линейно упорядочено и любое
непустое его подмножество имеет
наименьший элемент.
Утверждение.
Линейно упорядоченное множество является
вполне упорядоченным, если и только
если оно не содержит бесконечных
убывающих последовательностей элементов
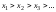
Доказательство.
Необходимость.
Пусть
 вполне упорядочено и в нём есть убывающая
цепь
вполне упорядочено и в нём есть убывающая
цепь Тогда множество
Тогда множество
 не имеет наименьшего элемента –
противоречие.
не имеет наименьшего элемента –
противоречие.
Достаточность.
Пусть
 – линейно упорядоченное множество без
бесконечных убывающих цепей элементов.
Рассмотрим какое-нибудь непустое
подмножество
– линейно упорядоченное множество без
бесконечных убывающих цепей элементов.
Рассмотрим какое-нибудь непустое
подмножество Пусть
Пусть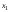 – какой-нибудь элемент из
– какой-нибудь элемент из Еслих1
не наименьший, то существует
Еслих1
не наименьший, то существует
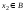 такое, что
такое, что Если
Если не наименьший, то существует
не наименьший, то существует такое, что
такое, что и т.д. Если
и т.д. Если не имеет наименьшего элемента, то
существует бесконечная убывающая цепь
не имеет наименьшего элемента, то
существует бесконечная убывающая цепь ,
что противоречит условию.
,
что противоречит условию.
Пр.1.Множество натуральных чисел с обычным отношением порядка является вполне упорядоченным.
Свойства вполне упорядоченных множеств:
любое подмножество вполне упорядоченного множества вполне упорядочено;
если
 и
и – два непересекающихся вполне
упорядоченных множества, то порядок
на множестве
– два непересекающихся вполне
упорядоченных множества, то порядок
на множестве определённый следующим образом.
определённый следующим образом.
превращает
 во вполне упорядоченное множество.
во вполне упорядоченное множество.
Доказательство очевидно.
Пусть
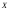 – линейно упорядоченное множество.Начальным
отрезком
множества
– линейно упорядоченное множество.Начальным
отрезком
множества
 назовём такое подмножество
назовём такое подмножество что
что
Лемма
1. Для любых
двух начальных отрезков
 линейно упорядоченного множества
линейно упорядоченного множества либо
либо либо
либо Доказательство.
Пусть
Доказательство.
Пусть
 Тогда существует
Тогда существует Возьмём любой элемент
Возьмём любой элемент Если бы
Если бы то
то что невозможно. Значит,
что невозможно. Значит, Отсюда следует, что
Отсюда следует, что Итак, любой элемент
Итак, любой элемент лежит в
лежит в Следовательно,
Следовательно,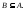
Два линейно упорядоченных множества называются изоморфными, если между ними существует взаимно однозначное соответствие, сохраняющее порядок.
Теорема
1. Для любых
двух вполне упорядоченных множеств
одно из них изоморфно начальному отрезку
другого. Доказательство.
Пусть
 – вполне упорядоченные множества.
Рассмотрим изоморфизмы
– вполне упорядоченные множества.
Рассмотрим изоморфизмы где
где – начальные отрезки множеств
– начальные отрезки множеств Такие изоморфизмы есть. Например, если
Такие изоморфизмы есть. Например, если и
и непусты, а
непусты, а и
и – наименьшие элементы множеств
– наименьшие элементы множеств и
и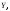 то
то – изоморфизм начальных отрезков. Докажем
теперь, что для каждого начального
отрезка
– изоморфизм начальных отрезков. Докажем
теперь, что для каждого начального
отрезка множества
множества изоморфизм
изоморфизм где
где – начальный отрезок множества
– начальный отрезок множества если существует, то однозначен.
Действительно, пусть
если существует, то однозначен.
Действительно, пусть
 – изоморфизмы, где
– изоморфизмы, где – начальный отрезок множества
– начальный отрезок множества Пусть
Пусть – наименьший элемент из
– наименьший элемент из такой, что
такой, что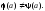 Мы можем считать, что
Мы можем считать, что Положим
Положим


 Очевидно,
Очевидно, отображает взаимно однозначно
отображает взаимно однозначно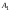 на
на Для
Для
 По условию
По условию и
и Поэтому
Поэтому при некотором
при некотором Имеем:
Имеем: что противоречит равенству
что противоречит равенству
Пусть
 – объединение всех начальных отрезков
– объединение всех начальных отрезков для которых существует изоморфизм
для которых существует изоморфизм на начальный отрезок
на начальный отрезок множества
множества Рассмотрим отображение
Рассмотрим отображение определённое следующим образом: если
определённое следующим образом: если то
то для некоторого
для некоторого для которого есть изоморфизм
для которого есть изоморфизм положим
положим Это определение является корректным,
так как если
Это определение является корректным,
так как если и
и – изоморфизм, то либо
– изоморфизм, то либо либо
либо Если
Если то
то и
и – изоморфизмы начального отрезка
– изоморфизмы начального отрезка на начальный отрезок
на начальный отрезок или
или Поэтому
Поэтому Значит,
Значит, что доказывает корректность определения
отображения
что доказывает корректность определения
отображения
Очевидно,
 – наибольший начальный отрезок в
– наибольший начальный отрезок в отображающийся на начальный отрезок в
отображающийся на начальный отрезок в Пусть
Пусть Докажем, что либо
Докажем, что либо либо
либо Предположим, что
Предположим, что и
и Пусть
Пусть
 Положим
Положим
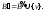 Очевидно,
Очевидно, и
и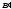 – начальные отрезки множеств
– начальные отрезки множеств и
и соответственно. Определим отображение
соответственно. Определим отображение положив
положив для
для и
и Очевидно,
Очевидно, – изоморфизм начальных отрезков
– изоморфизм начальных отрезков и
и Так как
Так как – наибольший начальный отрезок,
изоморфный начальному отрезку в
– наибольший начальный отрезок,
изоморфный начальному отрезку в то
то Однако
Однако Мы получили противоречие. Следовательно,
Мы получили противоречие. Следовательно,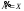 или
или В первом случае множество
В первом случае множество изоморфно начальному отрезку множества
изоморфно начальному отрезку множества во втором случае – наоборот. Теорема
доказана.
во втором случае – наоборот. Теорема
доказана.
