- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
10. Теорема Шрёдера – Бернштейна.
Мощностью
конечного множества мы будем называть
количество его элементов. Множества
 и
и
 называютсяэквивалентными
(или равномощными),
если существует взаимно однозначное
отображение множества
называютсяэквивалентными
(или равномощными),
если существует взаимно однозначное
отображение множества
 на множество
на множество Для эквивалентных множеств мы будем
писать
Для эквивалентных множеств мы будем
писать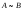 или
или
Свойства эквивалентности множеств:
1)

если
 то
то
если
 а
а то
то
Мощностью
множества А
называется
совокупность всех множеств, эквивалентных
множеству А.
Мощность множества А
обозначается

Говорят,
что мощность
множества
 не превосходит мощности множества
не превосходит мощности множества (записываем:
(записываем:
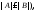 если
существует вложение множества
если
существует вложение множества
 в множество
в множество Если существует вложение
Если существует вложение
 в
в но не существует взаимно однозначного
отображения
но не существует взаимно однозначного
отображения на
на то мы говорим, что мощность множества
то мы говорим, что мощность множества строго меньше
мощности множества
строго меньше
мощности множества
 и пишем
и пишем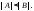
Теорема
1 (теорема Шрёдера – Бернштейна).
Если существуют вложения
 и
и то существует взаимно однозначное
отображение
то существует взаимно однозначное
отображение
Доказательство.
Положим

 Пусть
Пусть


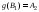 и вообще
и вообще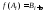
 Мы имеем:
Мы имеем:
 (1)
, где
(1)
, где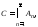
 (2)
, где
(2)
, где Очевидно,
Очевидно, взаимно однозначно отображает
взаимно однозначно отображает на
на поэтому существует
поэтому существует также взаимно однозначное. Проверим,
что
также взаимно однозначное. Проверим,
что взаимно однозначно отображает
взаимно однозначно отображает на
на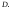 Действительно, пусть
Действительно, пусть Так как
Так как то
то
 Следовательно,
Следовательно,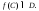 Пусть
Пусть Так как
Так как и
и то
то для некоторого
для некоторого Это равенство выполнено для каждого
натурального
Это равенство выполнено для каждого
натурального Если
Если
 и
и то (ввиду того, что
то (ввиду того, что – вложение)
– вложение) Следовательно,
Следовательно,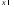
 Таким образом,
Таким образом,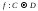 взаимно однозначно. Кроме того,
взаимно однозначно. Кроме того, взаимно однозначно отображает
взаимно однозначно отображает на
на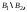
 на
на и т.д., а
и т.д., а взаимно однозначно отображает
взаимно однозначно отображает на
на
 на
на и т.д. Пользуясь соотношениями (1) и (2),
нетрудно убедиться в том, что отображение
и т.д. Пользуясь соотношениями (1) и (2),
нетрудно убедиться в том, что отображение определённое правилом
определённое правилом является взаимно однозначным. ЧТД.
является взаимно однозначным. ЧТД.
Практическое
значение: она позволяет доказывать
эквивалентность множеств
 и
и не прибегая к построению взаимно
однозначного отображения
не прибегая к построению взаимно
однозначного отображения а строя лишь вложения
а строя лишь вложения и
и
Пример.
Докажем, что отрезок
 и интервал
и интервал равномощны. Действительно,
тождественное отображение
равномощны. Действительно,
тождественное отображение является вложением
является вложением в
в Далее, отрезок
Далее, отрезок вкладывается в интервал
вкладывается в интервал а он взаимно однозначно отображается
на интервал
а он взаимно однозначно отображается
на интервал с помощью отображения
с помощью отображения Отсюда по теореме Шрёдера – Бернштейна
получаем:
Отсюда по теореме Шрёдера – Бернштейна
получаем: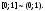
Итак,
отношение
 обладает обычными свойствами частичного
порядка (рефлексивность, транзитивность,
антисимметричность). Любые ли два
множества сравнимы по мощности,т.е.
верно ли, что для любых множеств
обладает обычными свойствами частичного
порядка (рефлексивность, транзитивность,
антисимметричность). Любые ли два
множества сравнимы по мощности,т.е.
верно ли, что для любых множеств и
и хотя бы одно из них вкладывается в
другое? Да,для
любых множеств А и В имеет место хотя
бы одно из следующих соотношений:
хотя бы одно из них вкладывается в
другое? Да,для
любых множеств А и В имеет место хотя
бы одно из следующих соотношений:

 но доказать это мы сможем лишь позже
– в разделе 2.2.
но доказать это мы сможем лишь позже
– в разделе 2.2.
11. Счетные множества и их свойства.
Определение.
Множество
 называетсясчётным,
если
называетсясчётным,
если
 N.
N.
Например,
счётным является множество 2N
чётных натуральных чисел. Действительно,
отображение
 задаёт взаимно однозначное соответствие
между множествамиN
и 2N.
задаёт взаимно однозначное соответствие
между множествамиN
и 2N.
Свойства счётных множеств:
объединение двух счётных множеств счётно;
прямое произведение двух счётных множеств счётно;
объединение счётного числа счётных множеств счётно;
всякое бесконечное множество имеет счётное подмножество.
Доказательство.
Докажем вначале утверждение 2). Пусть
 где
где счётные множества. Элементы множества
счётные множества. Элементы множества можно расположить в виде таблицы:
можно расположить в виде таблицы:
|
|
|
|
. . . |
|
|
|
|
. . . |
|
|
|
|
. . . |
|
. . . |
. . . |
. . . |
. . . |
Пересчёт
элементов множества
 т.е. установление взаимно однозначного
соответствия между элементами множеств
т.е. установление взаимно однозначного
соответствия между элементами множеств иN
может быть осуществлён, например, так:
иN
может быть осуществлён, например, так:
|
1 |
2 |
4 |
7 |
11 |
16 . . . |
|
3 |
5 |
8 |
12 |
17 |
23 . . . |
|
6 |
9 |
13 |
18 |
24 |
31 . . . |
|
10 |
14 |
19 |
25 |
32 |
40 . . . |
|
15 |
20 |
25 |
33 |
41 |
50 . . . |
|
21 . . . |
27 . . . |
34 . . . |
42 . . . |
51 . . . |
. . . . . . |
Номер,
который будет присвоен паре
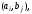 равен
равен
Утверждение
3) следует из 2) и теоремы Шрёдера –
Бернштейна. Поясним это. Пусть
 где каждое
где каждое счётно. Так какN
вкладывается в
счётно. Так какN
вкладывается в
 тоN
вкладывается в
тоN
вкладывается в
 Осталось построить вложение
Осталось построить вложение N.
По условию
N.
По условию
 счётные множества, поэтому
счётные множества, поэтому значит, элемент из
значит, элемент из имеет вид
имеет вид Не исключается, что
Не исключается, что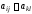 при каких-нибудь
при каких-нибудь Для каждого
Для каждого выберем одно какое-нибудь представление
в виде
выберем одно какое-нибудь представление
в виде Отображение
Отображение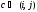 определяет вложение
определяет вложение вN
вN N,
а по свойству 2) | N
N,
а по свойству 2) | N N
| = | N
|. Значит,
N
| = | N
|. Значит,
 N
|.
N
|.
Утверждение
1) следует из 3), так как

Докажем
утверждение 4). Пусть
 бесконечное множество. Выберем элемент
бесконечное множество. Выберем элемент Так как
Так как бесконечно, то
бесконечно, то Значит, существует элемент
Значит, существует элемент Таким же образом найдём
Таким же образом найдём
 и т.д. Мы получили счётное подмножество
и т.д. Мы получили счётное подмножество множества
множества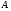 Мощность множестваN
(а значит, любого счётного множества)
обозначается
Мощность множестваN
(а значит, любого счётного множества)
обозначается  (читается: “алеф-нуль”). Так как всякое
бесконечное множество содержит счётное
подмножество, то
(читается: “алеф-нуль”). Так как всякое
бесконечное множество содержит счётное
подмножество, то  – самая маленькая из всех бесконечных
мощностей.
– самая маленькая из всех бесконечных
мощностей.
Если
 и
и – два непересекающихся счётных множества,
то по свойству 1)
– два непересекающихся счётных множества,
то по свойству 1)
 .
Это можно записать так:
.
Это можно записать так:  +
+
 =
=  .
Аналогично этому свойство 2) можно
записать так:
.
Аналогично этому свойство 2) можно
записать так: