7. Разрешимость классического исчисления высказываний.

Под разрешимостью мы понимаем существование алгоритма, который по данной формуле (или секвенцииопределяет, доказуема эта формула (или секвенция) или нет. Такой алгоритм действительно существует.

Теорема 4. Исчисление высказываний разрешимо.

Доказательство. По теореме 3 (о полноте ИВ: (а) Формула исчисления высказываний доказуема тогда и только тогда, когда она тождественно истинна. (б) Секвенция ИВ доказуема тогда и только тогда, когда она тождественно истинна.) проверка доказуемости формулы или секвенции сводится к проверке её тождественной истинности. Алгоритм такой проверки очевиден: надо придавать пропозициональным переменным входящим в рассматриваемые формулы, всевозможные значения(из множестваи определять по таблицам истинности значение формулы(соответственно, секвенцииЕсли на любом наборе будем иметь(соответственно,то(соответственно,тождественно истинна, а значит, доказуема, в противном случае(илинедоказуема.

Замечание. Пусть формула тождественно истинна, в чём мы убедились, применив алгоритм, изложенный в теореме 4. Тогдаимеет доказательство. На самом делеможно построить алгоритм, выписывающий это доказательство (т.е. доказательство секвенции Алгоритм достаточно громоздкий, так как включает в себя (в качестве “подпрограмм”) доказательства утвержденийи многих других, ведь мы приводим формулук видудоказываем формулузатем продолжаем доказательство, пока не будет доказана формула

8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.

Голландский математик Брауэр решил, что нельзя использовать в рассуждениях закон исключённого третьего, так как он предполагает, что любое суждение либо истинно, либо ложно, а это, по мнению Брауэра, противоречитинтуиции. Брауэр считал, что математика в своих абстрактных рассуждениях оторвалась от интуитивных корней и поэтому её выводы оказались неверными. Он считал, что следует очистить математику от неправильных (по его мнению) рассуждений и, в частности, убрать из математической практики закон исключённого третьего. Возражения против этого закона следующие: если мы утверждаем, что верно, то надо предъявить доказательство утвержденияа если мы утверждаем, чтоневерно, надо предъявить доказательство утвержденияговорить же о том, что обязательно либолибоокажется истинным, по мнению Брауэра, неправомерно. Это направление в математике и математической логике получило название интуиционизма. После Брауэра интуиционистские идеи были подхвачены Гейтингом и некоторыми другими математиками. В нашей стране идеи, близкие к интуиционистским, нашли выражение в конструктивизме, в создании которого большую роль сыграл А.А.Марков. Конструктивисты пошли дальше интуиционистов и требовали ещё больших ограничений в использовании логических средств.

Приведём некоторые результаты интуиционистской логики, созданной Гейтингом. Напомним, что она определяется гильбертовскими аксиомами (1) – (10) , а значит, нельзя использовать аксиому (11) – закон исключённого третьего.

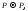
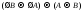Многие результаты исчислений гильбертовского типа верны не только в классической, но и в ИЛ. В частности, вывод формулы лемма о дедукции, “разбор случаев” не требовали применения закона исключённого третьего, а значит, справедливы в интуиционистской логике. Формулыдоказывались также без использования аксиомы (11), поэтому справедливы в ИИВ. Обратные формулысправедливы в классическом ИВ, но несправедливы в интуиционистском. Итак, в ИЛ двойное отрицание неэквивалентно отсутствию отрицания. Однакотройное отрицание эквивалентно однократному. Действительно, в доказательстве формулы можно сразу вместовзятьи мы получим:Возьмём в формулевместоформулуТогда получим:Так какуже доказано, то поmodus ponens получим:

Один из законов де-Моргана, а именно: исправедлив в ИИВ, так как его доказательство не использует закон исключённого третьего. Другой закон де-Моргана в интуиционистской логике несправедлив.

Приведём примеры формул, не выводимых в интуиционистской логике (здесь – атомарные формулы):

Подчеркнём, что невыводимость перечисленных формул гарантируется лишь в случае, когда и– атомарные формулы. Если – неатомарные, то некоторые из перечисленных формул могут оказаться выводимыми; например, если во второй формуле вместовзятьто получится выводимая в ИИВ формула

Докажем теперь невыводимость формулы 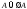(закона исключённого третьего) в интуиционистской логике. Рассмотрим трёхзначное множество значений истинности в котором 0 интерпретируется как ложь (Л), 1 – как истина (И), 1/2– как неопределённость (Н). Определим конъюнкцию и дизъюнкцию обычным способом:отрицание:Импликация определяется так:

Можно проверить, что аксиомы гильбертова исчисления (1) – (10) являются тождественно истинными в трёхзначной логике, т.е. при любом присвоении буквам значений из множестваформула оказывается равной 1. Кроме того, правилоmodus ponens сохраняет тождественную истинность. Значит, все выводимые в ИИВ формулы тождественно истинны (в трёхзначной логике). Однако, формула тождественно истинной не является, так как приННН = Н И. Значит, формула невыводима в ИИВ. (отрицание неопределённости=ложь)