
- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
6. Теорема о полноте.
Рассмотрим
теперь главную
интерпретацию ИВ.
Это будет отображение
 где
где – множество всех формул, а
– множество всех формул, а – множество всех секвенций. Для атомарных
формул
– множество всех секвенций. Для атомарных
формул значения
значения выберем произвольным образом. На
остальные формулы отображение
выберем произвольным образом. На
остальные формулы отображение распространим по обычным правилам:
распространим по обычным правилам:
 где
где Отображение
Отображение можно рассматривать как присвоение
значений истинности (“истина” или
“ложь”) пропозициональным переменным.
После того, как такое присвоение
произошло, можно говорить об истинности
или ложности других формул. Истинность
или ложность секвенций определяется
следующим образом:
можно рассматривать как присвоение
значений истинности (“истина” или
“ложь”) пропозициональным переменным.
После того, как такое присвоение
произошло, можно говорить об истинности
или ложности других формул. Истинность
или ложность секвенций определяется
следующим образом:
 либо
либо
 при некотором
при некотором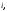 либо
либо



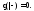
Сформулируем
теперь эти определения другими словами.
Пусть
 – формула ИВ, зависящая от пропозициональных
переменных (атомарных формул)
– формула ИВ, зависящая от пропозициональных
переменных (атомарных формул)
 а
а – набор из 0 и 1. Будем говорить, чтоформула
– набор из 0 и 1. Будем говорить, чтоформула
 истинна на наборе
истинна на наборе если
если
 при
при . . . ,
. . . ,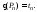 Пусть дана секвенция
Пусть дана секвенция и
и – пропозициональные переменные, входящие
в какие-либо из формул
– пропозициональные переменные, входящие
в какие-либо из формул Секвенция
Секвенция истинна на
наборе
истинна на
наборе
 из 0 и 1, если на этом наборе либо хотя бы
одно из
из 0 и 1, если на этом наборе либо хотя бы
одно из ложно, либо
ложно, либо истинно. Далее, секвенция
истинно. Далее, секвенция истинна на
наборе
истинна на
наборе
 если хотя бы одна из формул
если хотя бы одна из формул на этом наборе ложна. Секвенция
на этом наборе ложна. Секвенция истинна на
данном наборе,
если на этом наборе
истинна на
данном наборе,
если на этом наборе
 истинно. Наконец, секвенция
истинно. Наконец, секвенция считаетсяложной
на любом наборе.
считаетсяложной
на любом наборе.
Отметим,
что главная интерпретация является
частным случаем интерпретации,
рассмотренной ранее. Действительно,
пусть
 состоит из одного элемента. Тогда
состоит из одного элемента. Тогда Считаем для ф-лы
Считаем для ф-лы
 если
если и
и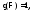 если
если Непосредственно проверяется, что
получится главная интерпретация.
Непосредственно проверяется, что
получится главная интерпретация.
Формула
 (соответственно, секвенция
(соответственно, секвенция )
называетсятождественно
истинной,
если она истинна на любом наборе значений
истинности пропозициональных переменных.
Нетрудно видеть, что тождественная
истинность формулы
)
называетсятождественно
истинной,
если она истинна на любом наборе значений
истинности пропозициональных переменных.
Нетрудно видеть, что тождественная
истинность формулы
 равносильна тождественной истинности
секвенции
равносильна тождественной истинности
секвенции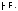
Лемма
1. Секвенция
 истинна на наборе
истинна на наборе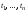 в том итолько
в том случае, если секвенция
в том итолько
в том случае, если секвенция
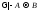 истинна на этом наборе.
истинна на этом наборе.
Док-во.
Пусть
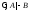 истинна на наборе
истинна на наборе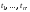 Тогда выполняется хотя бы одно из
условий: 1) хотя бы одна из формул множества
Тогда выполняется хотя бы одно из
условий: 1) хотя бы одна из формул множества ложна на этом наборе; 2) формула
ложна на этом наборе; 2) формула ложна на этом наборе; 3) формула
ложна на этом наборе; 3) формула истинна на этом наборе. Разберём эти
случаи отдельно. 1) Если какая-нибудь
формула из
истинна на этом наборе. Разберём эти
случаи отдельно. 1) Если какая-нибудь
формула из ложна, то
ложна, то истинна, а значит,
истинна, а значит, истинна. 2) Если
истинна. 2) Если ложна, то
ложна, то истинна, поэтому
истинна, поэтому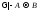 истинна. 3) Если
истинна. 3) Если истинна, то
истинна, то истинна, а значит,
истинна, а значит, также истинна.
также истинна.
Следствие.
Секвенция
 тождественно истинна только в том
случае, если секвенция
тождественно истинна только в том
случае, если секвенция тождественно истинна.
тождественно истинна.
Лемма
2. Секвенция
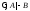 доказуема только в том случае, если
секвенция
доказуема только в том случае, если
секвенция доказуема.
доказуема.
Док-во.
Если секвенция
 имеет доказательство, то по правилу 7
это доказательство можно продолжить и
получить
имеет доказательство, то по правилу 7
это доказательство можно продолжить и
получить Наоборот, если доказана секвенция
Наоборот, если доказана секвенция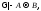 то из неё по правилу 12 получим
то из неё по правилу 12 получим Учитывая легко доказываемый факт
Учитывая легко доказываемый факт по правилу 8 получим
по правилу 8 получим
Лемма
3. а) Если
секвенция
 доказуема, то она тождественно истинна;
доказуема, то она тождественно истинна;
б)
если формула
 доказуема, то она тождественно истинна.
доказуема, то она тождественно истинна.
Док-во. Нетрудно проверить, что аксиомы являются тождественно-истинными секвенциями. Также легко проверяется, что применение правил вывода эту тождественную истинность не нарушает. Значит, любая выводимая (доказуемая) секвенция тождественно истинна. Утверждение, касающееся формул, сводится к уже доказанному для секвенций.
Лемма
4. Если
формулы
 и
и эквивалентны, то булевы функции
эквивалентны, то булевы функции и
и совпадают.
совпадают.
Док-во.
Можно считать, что формулы
 и
и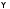 зависят от одних и тех же пропозициональных
переменных
зависят от одних и тех же пропозициональных
переменных (переменные, которые не входят в формулу,
считаем входящими фиктивно). По условию
(переменные, которые не входят в формулу,
считаем входящими фиктивно). По условию и
и – доказуемые секвенции. По лемме 3 они
тождественно истинны. Если на каком-либо
наборе
– доказуемые секвенции. По лемме 3 они
тождественно истинны. Если на каком-либо
наборе формула
формула истинна, то так как секвенция
истинна, то так как секвенция истинна, то
истинна, то на этом наборе тоже истинна. Аналогично
доказывается, что если
на этом наборе тоже истинна. Аналогично
доказывается, что если истинна на наборе
истинна на наборе то
то также истинна на этом наборе. Итак,
также истинна на этом наборе. Итак, и
и истинны на одних и тех же наборах, значит,
истинны на одних и тех же наборах, значит,
Для
формулы
 обозначим через
обозначим через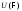 множество наборов
множество наборов на которых она истинна.
на которых она истинна.
Замечание.
Лемма 4 на самом деле является следствием
более общего результата: если для
некоторых формул
 и
и секвенция
секвенция доказуема, то
доказуема, то
Теорема
2 (о
функциональной полноте ИВ).
Пусть в исчислении высказываний
бесконечно много атомарных формул.
Тогда для любой булевой функции
 существует формула
существует формула исчисления высказываний, зависящая от
атомарных формул
исчисления высказываний, зависящая от
атомарных формул такая, что
такая, что
Доказательство.
Если
 тождественно равна 0, то в качестве
формулы
тождественно равна 0, то в качестве
формулы можно взять
можно взять Если же
Если же то, как известно из курса дискретной
математики,
то, как известно из курса дискретной
математики, представима в совершенной дизъюнктивной
нормальной форме:
представима в совершенной дизъюнктивной
нормальной форме:



Следовательно,
в качестве формулы
 исчисления высказываний подойдёт
формула
исчисления высказываний подойдёт
формула


Из леммы 3 мы видели, что доказуемыми могут быть только тождественно истинные формулы или секвенции. Оказывается (и это мы докажем в следующей теореме), что верно и обратное: тождественно истинная формула или секвенция имеет формальное доказательство в ИВ. Этот факт мы будем называть полнотой исчисления высказываний.
Теорема 3 (о полноте ИВ).
(а) Формула исчисления высказываний доказуема тогда и только тогда, когда она тождественно истинна.
(б) Секвенция ИВ доказуема тогда и только тогда, когда она тождественно истинна.
Доказательство.
Ввиду леммы 2 и следствия из леммы 1
доказуемости (соответственно, тождественные
истинности) следующих секвенций
эквивалентны:


 . . . Таким образом можно “перебросить”
все формулы, стоящие слева от значка
. . . Таким образом можно “перебросить”
все формулы, стоящие слева от значка в правую часть и получить секвенцию
вида
в правую часть и получить секвенцию
вида для которой доказуемость (соответственно,
тождественная истинность) равносильна
доказуемости (соответственно, тождественной
истинности) формулы
для которой доказуемость (соответственно,
тождественная истинность) равносильна
доказуемости (соответственно, тождественной
истинности) формулы (по определению). Следовательно, нам
надо доказать только утверждение (а).
(по определению). Следовательно, нам
надо доказать только утверждение (а).
Ввиду
леммы 3 нам следует доказать лишь
достаточность: если формула
 тождественно истинна, то она доказуема.
Пусть
тождественно истинна, то она доказуема.
Пусть – тождественно истинная формула. По
теореме 2 предыдущего раздела существует
формула
– тождественно истинная формула. По
теореме 2 предыдущего раздела существует
формула такая, что
такая, что


Положим
 . . . ,
. . . , Так как
Так как то по лемме 4
то по лемме 4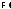 тождественно истинна. Но это означает,
что формулы
тождественно истинна. Но это означает,
что формулы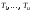 тождественно истинны. Рассмотрим
какую-нибудь одну из них, например,
тождественно истинны. Рассмотрим
какую-нибудь одну из них, например, Если все
Если все различны, то
различны, то не будет тождественно истинной, так как
обращается в 0 на таком наборе, где
не будет тождественно истинной, так как
обращается в 0 на таком наборе, где Значит, в
Значит, в какая-либо пропозициональная переменная
(скажем,
какая-либо пропозициональная переменная
(скажем, встречается вместе со своим отрицанием.
Следовательно,
встречается вместе со своим отрицанием.
Следовательно, можно преобразовать:
можно преобразовать: Секвенция
Секвенция
 доказуема по лемме 4 § 1.1. По правилу
вывода 4 получим,
что секвенция
доказуема по лемме 4 § 1.1. По правилу
вывода 4 получим,
что секвенция
 доказуема. Значит, формула
доказуема. Значит, формула доказуема. Аналогично получим, что
формулы
доказуема. Аналогично получим, что
формулы доказуемы. По правилу 1 получим, что
формула
доказуемы. По правилу 1 получим, что
формула доказуема. Следовательно, формула
доказуема. Следовательно, формула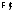 а значит, и формула
а значит, и формула доказуема.
доказуема.
