
- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
33. Оператор минимизации. Рекурсивные функции.
34. Разрешимые и перечислимые множества. Характеризация перечислимых множеств.
35. Универсальные вычислимые функции.
36. Существование перечислимого неразрешимого множества.
37. Алгоритмически неразрешимые задачи. Неразрешимость проблемы остановки машины Тьюринга.
38.
Сложность алгоритмов. Гипотеза
СТАРЫЕ ОТВЕТЫ
32. Примитивно рекурсивные и рекурсивные функции.
Напомним,
что в этой главе множество N
натуральных чисел содержит 0, т.е.
 Будем рассматривать функции (возможно,
частичные)
Будем рассматривать функции (возможно,
частичные)
 Таким образом, если
Таким образом, если то либо
то либо либо
либо не определено. Введём в рассмотрениепростейшие
функции о
не определено. Введём в рассмотрениепростейшие
функции о s
s I
I
Эти ф-ции могут быть вычислены с помощью соотв. механического устройства (например, на м. Тьюринга). Определим операторы, кот. по одной или неск-ким заданным функциям строят новые ф-ции.
Оператор
суперпозиции.
Пусть даны функция
 от
от переменных и
переменных и функций
функций от
от переменных.. Суперпозицией функций
переменных.. Суперпозицией функций называется функция
называется функция

Мы
говорим, что функция
 получается применением оператора
суперпозиции
получается применением оператора
суперпозиции к функциям
к функциям и пишем
и пишем
Например,
 (s,o)
– это функция
(s,o)
– это функция
 s(o
s(o т.е. функция, тождественно равная 1, а
т.е. функция, тождественно равная 1, а
 (s,s)
– это функция
(s,s)
– это функция

Оператор
примитивной рекурсии.
Пусть даны функции
 и
и Построим функцию
Построим функцию Пусть зафиксированы значения
Пусть зафиксированы значения Тогда положим:
Тогда положим:

Эти равенства определяют функцию
 однозначно. Функция
однозначно. Функция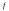 называется функцией, полученной с
помощью оператора
называется функцией, полученной с
помощью оператора примитивной рекурсии. Используется
запись
примитивной рекурсии. Используется
запись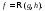
Индуктивное
определение функции (продемонстрированное
в операторе примитивной рекурсии) в
математике не редкость. Например,
индуктивно определяются степень с
натуральным показателем:

 факториал:
факториал:
 и т.д.
и т.д.
Функции,
которые могут быть получены из простейших
о s
s I
I применением конечного числа раз
операторов суперпозиции и примитивной
рекурсии, называются примитивно
рекурсивными.
(примитивно рекурсивные функции всюду
определен, т.е.
определены для всех значений их
аргументов). Существенно более широким
классом функций, чем примитивно
рекурсивные функции, является класс
рекурсивных
функций (определение см. ниже). В
литературе эти функции называют также
частично
рекурсивными.
Для их определения введём ещё один
оператор.
применением конечного числа раз
операторов суперпозиции и примитивной
рекурсии, называются примитивно
рекурсивными.
(примитивно рекурсивные функции всюду
определен, т.е.
определены для всех значений их
аргументов). Существенно более широким
классом функций, чем примитивно
рекурсивные функции, является класс
рекурсивных
функций (определение см. ниже). В
литературе эти функции называют также
частично
рекурсивными.
Для их определения введём ещё один
оператор.
Оператор
минимизации.
Пусть дана функция
 Зафиксируем какие-либо значения
Зафиксируем какие-либо значения первых
первых переменных и будем вычислять
переменных и будем вычислять
 и т.д. Если
и т.д. Если наименьшее натуральное число, для
которого
наименьшее натуральное число, для
которого (т.е. значения
(т.е. значения
 все существуют и не равны
все существуют и не равны то полагаем
то полагаем Таким образом,
Таким образом,


Если
такого
 нет, то считаем, что
нет, то считаем, что не определено. Итак, возможны три случая:
не определено. Итак, возможны три случая:

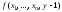 существуют
и не равны
существуют
и не равны
 а
а

 существуют
и не равны
существуют
и не равны
 а
а не существует;
не существует; существуют
при всех
существуют
при всех
 и отличны от
и отличны от
Если
имеет место 1-й случай, то
 а если 2-й или 3-й, то
а если 2-й или 3-й, то не определено. Про функцию
не определено. Про функцию полученную таким образом, говорят, что
она получена из
полученную таким образом, говорят, что
она получена из применением оператора минимизации
применением оператора минимизации Мы пишем
Мы пишем
Функции,
которые могут быть получены из простейших
о s
s I
I применением конечного числа раз
операторов суперпозиции, примитивной
рекурсии и минимизации, называются
рекурсивными.
применением конечного числа раз
операторов суперпозиции, примитивной
рекурсии и минимизации, называются
рекурсивными.
33. Разрешимые множества и их свойства.
Множество
 натуральных чисел называетсяразрешимым,
если существует алгоритм, который по
каждому натуральному числу
натуральных чисел называетсяразрешимым,
если существует алгоритм, который по
каждому натуральному числу
 определяет, принадлежит
определяет, принадлежит множеству
множеству или не принадлежит. Другими словами,
множество
или не принадлежит. Другими словами,
множество разрешимо в том и только в том случае,
если егохарактеристическая
функция
разрешимо в том и только в том случае,
если егохарактеристическая
функция
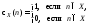 вычислима.
вычислима.
Понятно,
что если множества
 и
и разрешимы, то множества
разрешимы, то множества

 также разрешимы. Любое конечное множество
является разрешимым. Неразрешимые
множества также существуют, так как
разрешимые подмножества образуют
счётное множество, а все подмножества
множества натуральных чисел образуют
множество мощности континуума.
также разрешимы. Любое конечное множество
является разрешимым. Неразрешимые
множества также существуют, так как
разрешимые подмножества образуют
счётное множество, а все подмножества
множества натуральных чисел образуют
множество мощности континуума.
Теорема
3. Всякое
разрешимое множество натуральных чисел
перечислимо. Если множество
 и его дополнениеN\A
перечислимы, то
и его дополнениеN\A
перечислимы, то
 разрешимо.
разрешимо.
Доказательство.
Пусть
 – разрешимое множество натуральных
чисел. Тогда существует машина Тьюринга
– разрешимое множество натуральных
чисел. Тогда существует машина Тьюринга которая, имея на входе число
которая, имея на входе число выдаёт на выходе 1 при
выдаёт на выходе 1 при и 0 при
и 0 при Добавим к программе машины
Добавим к программе машины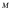 команды так, чтобы после перехода машины
команды так, чтобы после перехода машины в финальное состояние продолжение
работы было следующим: 1) если на выходе
1, машина заменяет её на 0 и завершает
работу, 2) если на выходе уже был 0, то
машина далее работает безостановочно
(например, движется направо и печатает
на ленте 1). Очевидно, построенная нами
машина вычисляет функцию
в финальное состояние продолжение
работы было следующим: 1) если на выходе
1, машина заменяет её на 0 и завершает
работу, 2) если на выходе уже был 0, то
машина далее работает безостановочно
(например, движется направо и печатает
на ленте 1). Очевидно, построенная нами
машина вычисляет функцию Значит, множество
Значит, множество перечислимо.
перечислимо.
Пусть
 иN\A
перечислимы, а
иN\A
перечислимы, а
 и
и – машины Тьюринга, вычисляющие
соответственно функции
– машины Тьюринга, вычисляющие
соответственно функции и
и Построим
новую машину Тьюринга
Построим
новую машину Тьюринга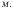 Она, имея на входе число
Она, имея на входе число делает
вначале один шаг работы машины
делает
вначале один шаг работы машины затем
один шаг работы
затем
один шаг работы затем два шага
затем два шага (начиная с первого), затем два шага
(начиная с первого), затем два шага и т.д. По завершению работы одной из
машин
и т.д. По завершению работы одной из
машин дальнейшие действия таковы: если
дальнейшие действия таковы: если завершила работу раньше, то заменяем
выходное значение 0 на 1 и производим
остановку машины, а если ранее завершится
программа
завершила работу раньше, то заменяем
выходное значение 0 на 1 и производим
остановку машины, а если ранее завершится
программа то производится просто остановка машины.
Легко видеть, что на выходе будет 1 при
то производится просто остановка машины.
Легко видеть, что на выходе будет 1 при и 0 при
и 0 при Остановка
произойдёт обязательно, так как по
условию обе функции
Остановка
произойдёт обязательно, так как по
условию обе функции
 и
и вычислимы.
вычислимы.
