
- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
25. Элиминация кванторов.
Пусть
 – модель (где
– модель (где – носитель,
– носитель, – сигнатура),
– сигнатура), –п-местный
предикат на множестве
–п-местный
предикат на множестве
 Мы будем говорить, что предикат
Мы будем говорить, что предикат выразим
в данной модели, если существует формула
выразим
в данной модели, если существует формула
 логики первого порядка такая, что
логики первого порядка такая, что

Приведём
теперь примеры невыразимых предикатов.
Простейшим примером
служит предикат
 в модели
в модели
 .
Действительно, интуитивно ясно, что
если в сигнатуре нет арифметических
операций, то все элементы множества Z
равноправны и отличить число 0 от других
чисел невозможно. Разумеется, эти
рассуждения не доказывают невыразимость
предиката
.
Действительно, интуитивно ясно, что
если в сигнатуре нет арифметических
операций, то все элементы множества Z
равноправны и отличить число 0 от других
чисел невозможно. Разумеется, эти
рассуждения не доказывают невыразимость
предиката

Автоморфизмом
модели
 называется взаимно однозначное
отображение
называется взаимно однозначное
отображение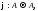 сохраняющее значения истинности всех
формул. В предыдущем примере автоморфизмом
было отображение
сохраняющее значения истинности всех
формул. В предыдущем примере автоморфизмом
было отображение
Две
формулы УИП мы будем называть
эквивалентными,
если они имеют один и тот же набор
свободных переменных и значения
истинности этих формул будут одинаковы,
какие бы значения из множества
 мы ни придали свободным переменным.
мы ни придали свободным переменным.
Оказывается, в некоторых моделях для всякой формулы УИП, содержащей кванторы, существует эквивалентная ей формула без кванторов. В этом случае мы будем говорить, что модель допускает элиминацию кванторов.
Теорема.
Модель

 где = – отношение равенства,
где = – отношение равенства, – унарная операция и 0 – нульарная
операция, допускает элиминацию кванторов.Доказательство.
Индукция по количеству кванторов в
формуле. От квантора
– унарная операция и 0 – нульарная
операция, допускает элиминацию кванторов.Доказательство.
Индукция по количеству кванторов в
формуле. От квантора
 в любой формуле можно избавиться, заменив
формулу
в любой формуле можно избавиться, заменив
формулу на эквивалентную ей формулу
на эквивалентную ей формулу Таким образом, нам достаточно доказать,
что формула
Таким образом, нам достаточно доказать,
что формула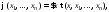 где
где не содержит кванторов, имеет эквивалентную
ей бескванторную формулу. Формула
не содержит кванторов, имеет эквивалентную
ей бескванторную формулу. Формула получается из атомарных формул с помощью
логических связок. Атомарные формулы,
содержащие переменную
получается из атомарных формул с помощью
логических связок. Атомарные формулы,
содержащие переменную имеют вид
имеют вид или
или или
или
Формула
первого типа либо тождественно истинна,
либо тождественно ложна, поэтому её
можно заменить на эквивалентную формулу,
не содержащую

 или
или Формулы второго и третьего типов можно
кратко записать в виде
Формулы второго и третьего типов можно
кратко записать в виде где
где или
или (
( – константа, не обязательно положительная),
– константа, не обязательно положительная),
Рассмотрим
формулу

Очевидно,
что если формула
 истинна на каком-либо наборе
истинна на каком-либо наборе то формула
то формула также истинна на этом наборе. Обратное
в общем случае неверно, так как
также истинна на этом наборе. Обратное
в общем случае неверно, так как может быть сделана истинной, когда
может быть сделана истинной, когда для некоторого
для некоторого отличного от всех
отличного от всех Но тогда все атомарные формулы
Но тогда все атомарные формулы ложны. Заменим каждую из этих формул на
какую-нибудь тождественно ложную формулу
и обозначим полученную формулу через
ложны. Заменим каждую из этих формул на
какую-нибудь тождественно ложную формулу
и обозначим полученную формулу через Тогда формула
Тогда формула будет эквивалентна формуле
будет эквивалентна формуле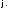
26. Фильтр. Центрированная система множеств.
Фильтром
на множестве
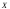 называется совокупность
называется совокупность подмножеств множества
подмножеств множества обладающая свойствами:
обладающая свойствами:
 (2)
(2)
 (3)
(3)

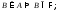
Примеры фильтров:
Пусть

 Тогда
Тогда – фильтр. Он называется фильтром,
порождённым множеством
– фильтр. Он называется фильтром,
порождённым множеством
Пусть
 Тогда
Тогда –
фильтр. Он называетсяглавным
фильтром,
порождённым элементом
–
фильтр. Он называетсяглавным
фильтром,
порождённым элементом
 (максимальный
по включению)
(максимальный
по включению)Пусть
 – бесконечное множество и
– бесконечное множество и – множество таких
– множество таких что
что Тогда
Тогда – фильтр.
– фильтр.
Пусть
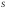 – совокупность подмножеств множества
– совокупность подмножеств множества
 .Она
называетсяцентрированной
системой
подмножеств
(или:
.Она
называетсяцентрированной
системой
подмножеств
(или:
 обладает свойством конечных пересечений),
если пересечение любого конечного числа
множеств из
обладает свойством конечных пересечений),
если пересечение любого конечного числа
множеств из
 непусто, т.е.
непусто, т.е.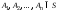


Теорема
1. Всякая
центрированная система подмножеств
вкладывается в фильтр.
Доказательство.
Пусть
 – центрированная система подмножеств
множества
– центрированная система подмножеств
множества Обозначим через
Обозначим через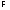 совокупность таких подмножеств
совокупность таких подмножеств множества
множества что
что для некоторых
для некоторых Проверим, что
Проверим, что – фильтр. Из определения системы
– фильтр. Из определения системы следует, что
следует, что при всех
при всех Значит,
Значит, Пусть
Пусть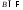 и
и Так
как
Так
как при некоторых
при некоторых
 то также
то также Значит,
Значит, Наконец, пусть
Наконец, пусть Тогда
Тогда
 при некоторых
при некоторых Следовательно,
Следовательно, а значит,
а значит,
