24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.

Сигнатурой называется пара где– набор символов операций– символ-арной операции),– набор символов отношений– символ-арного отношения).

Примеры сигнатур:

1. Группу можно рассматривать в сигнатуре (один символ бинарной операции – умножения и ни одного символа отношений) или в сигнатуре(один символ бинарной операции – умножения и один символ унарной операции – взятия обратного).

Пусть – сигнатура.Моделью сигнатуры называется множество такое, что каждому символу операциипоставлена в соответствие операция той же арности на множествеи каждому символу отношенияпоставлено в соответствие отношениетой же арности на множествеОперацию мы будем обозначать той же буквой, что и символ операции, а отношение – так же, как символ отношения. Множествомы будем называтьносителем модели. Нормальной является модель, в кот. Есть отношение «=», и оно понимается как совпадение элементов.

Примеры моделей:

1. Частично упорядоченное множество определяется как модель 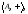где– символ бинарного отношения, удовлетворяющий следующим аксиомам:

1) (рефлексивность), 2) (транзитивность), 3) (антисимметричность). Если кроме этих аксиом выполняется аксиома 4) (дихотомичность), то называетсялинейно упорядоченным множеством, или цепью.

Пусть задана сигнатура т.е. множествосимволов операций и множествосимволов отношений.Язык логики первого порядка (язык узкого исчисления предикатов (УИП)) содержит:

1. символы из множеств и

2. алфавит предметных переменных; (маленькие буквы: алфавиткак правило, будет предполагаться счётным);

3. логические связки:

4. служебные символы: “,”, “(”, “)” (запятая, левая и правая скобки).

Терм определяется индуктивно:

1. предметная переменная – терм;

2. если – термы и– символп-арной операции, то – терм.

Примеры термов:

1. Для сигнатуры следующие выражения являются термами:Последний терм мы будем писать в сокращённом виде:а если имеет место ассоциативность умножения, то можно записать

Формула логики первого порядка сигнатуры определяется индуктивно:

1. если – термы сигнатурыи– символп-местного отношения, то – формула (такие формулы называютсяатомарными);

2. если и– формулы, то– формулы;

3. если – формула и– предметная переменная, тои– формулы.

Отметим, что так же, как и в исчислении высказываний, для облегчения восприятия формул мы часто в выражениях вида внешние скобки будем опускать.Примеры формул:

1. В сигнатуре формулами УИП являются слова:

2. В сигнатуре где точка обозначает символ бинарной операции, а = и– соответственно символы бинарного и тернарного отношений, примерами формул являются:

Связанная переменная формулы – это переменная которая связана квантором, т.е. в формулеесть подсловоилиПеременные, входящие в формулу, но не связанные кванторами, называютсясвободными. Формула называетсязамкнутой, если она не содержит свободных переменных. Замкнутую формулу можно назвать высказыванием. Незамкнутые формулы являются предикатами, но эти предикаты нульместные. Пример: – замкнутая формула, а– незамкнутая, её можно рассматривать как предикат от переменныхи(здесьозначает равенство по определению).Всякая формула УИП является предикатом от своих свободных переменных.

Пусть – модель, где– носитель,– сигнатура и– формула УИП со свободными переменнымиИстинность или ложность этой формулы зависит от того, какие значения мы придадим переменнымНазовёмоценкой отображение (смысл её состоит в том, что мы каждой предметной переменной присваиваем какое-то значение из множестваОпределимзначение истинности формулы на оценке Истину мы будем обозначать буквой И, а ложь – буквой Л. Определение построим индукцией по длине формулы. Положим ... ,

1. если – атомарная формула, где– термы, тов том и только в том случае, если

2. если имеет видилито истинность или ложность высказыванияопределяется по обычным правилам;

3. если тов том и только том случае, еслипри всех

если тов том и только том случае, еслипри каком-нибудь