
- •Вопросы
- •1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
- •2. Правила вывода. Секвенции. Доказательства.
- •4,5. Непротиворечивость классического ив.
- •6. Теорема о полноте.
- •7. Разрешимость классического исчисления высказываний.
- •8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •10. Теорема Шрёдера – Бернштейна.
- •11. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •12. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •13. Связь между счетными множествами и множествами мощности континуума.
- •14. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •15. Эквиваленстность множеств(см.Ниже)
- •16. Вполне упорядоченные множества и их свойства.
- •17. Аксиома выбора. Теорема Цермело.
- •18. Лемма Цорна.
- •19. Ординальные числа и их свойства.
- •20. Кардинальные числа и их свойства.
- •21. Мощность множества АхА
- •22. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •23. Аксиомы действительных чисел.
- •24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •25. Элиминация кванторов.
- •26. Фильтр. Центрированная система множеств.
- •27. Ультрафильтр. Характеризация ультрафильтров.
- •28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении.Th. Лося.
- •29. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
Вопросы
Вопросы 1
1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ИВ в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний. 2
2. Правила вывода. Секвенции. Доказательства. 4
4,5. Непротиворечивость классического ИВ. 6
6. Теорема о полноте. 8
7. Разрешимость классического исчисления высказываний. 11
8,9. Понятие об интуиционизме и конструктивизме в логике. Интуиционистское ИВ. Недоказуемость закона исключённого третьего. 12
10. Теорема Шрёдера – Бернштейна. 14
11. Счетные множества и их свойства. 16
12. Несчестность множества действительных чисел. Свойства множеств мощности континуума. 18
13. Связь между счетными множествами и множествами мощности континуума. 20
14. Теорема Кантора о мощности множества всех подмножеств данного множества. 21
15. Эквиваленстность множеств(см.ниже) 22
16. Вполне упорядоченные множества и их свойства. 23
17. Аксиома выбора. Теорема Цермело. 25
18. Лемма Цорна. 27
19. Ординальные числа и их свойства. 28
20. Кардинальные числа и их свойства. 31
21. Мощность множества АхА 32
22. Аксиомы Пеано натуральных чисел. Коммутативность сложения. 33
23. Аксиомы действительных чисел. 35
24. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели. 36
25. Элиминация кванторов. 39
26. Фильтр. Центрированная система множеств. 40
27. Ультрафильтр. Характеризация ультрафильтров. 41
28. Ультрапроизведение моделей. Истинность формул на ультрапроизведении. Th. Лося. 42
29. Теорема Гёделя – Мальцева и следствие из нее. 45
31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча. 46
1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ив в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
Алфавит ИВ содержит следующие символы:
пропозициональные переменные
 – они обозначают элементарные
высказывания – это “кирпичики”, из
которых будут формироваться другие,
более сложные высказывания;
– они обозначают элементарные
высказывания – это “кирпичики”, из
которых будут формироваться другие,
более сложные высказывания;логические связки:

служебные символы: “(“, “)”, “,” (левая скобка, правая скобка, запятая);
символ

Формула ИВ (высказывание) определяется индуктивно по следующей схеме:
атомарные формулы (простейшие) – это пропозициональные переменные;
если
 и
и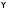 – формулы, то
– формулы, то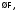


 – формулы.
– формулы.
Итак,
формулами ИВ называются только те слова,
записанные в алфавите ИВ, которые
получаются по вышеприведённой схеме.
Например, если
 – пропозициональные переменные, то
– пропозициональные переменные, то

 – формулы, а
– формулы, а


 – не формулы.
– не формулы.
Пусть
дано слово
 в алфавите
в алфавите Подсловом
этого слова мы называем всякое слово
вида
Подсловом
этого слова мы называем всякое слово
вида
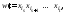 где
где началом
слова
началом
слова
 называется подслово вида
называется подслово вида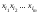
 Слово, в котором нет ни одной буквы,
называетсяпустым
словом
и обозначается символом
Слово, в котором нет ни одной буквы,
называетсяпустым
словом
и обозначается символом
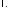 Пустое слово является подсловом любого
слова.Подформулой
формулы
Пустое слово является подсловом любого
слова.Подформулой
формулы
 мы будем называть подслово слова
мы будем называть подслово слова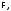 которое само является формулой.
которое само является формулой.
Лемма
1. Если
 и
и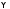 – формулы и
– формулы и – начало
– начало то
то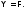 Доказательство
проведём индукцией по длине
формулы
Доказательство
проведём индукцией по длине
формулы
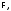 т.е. по количеству символов, входящих в
т.е. по количеству символов, входящих в Если длина равна 1, то
Если длина равна 1, то – атомарная формула, тогда
– атомарная формула, тогда тоже атомарная; очевидно, что
тоже атомарная; очевидно, что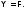 Если
Если не атомарна, то
не атомарна, то начинается либо с
начинается либо с либо с
либо с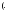 Пусть
Пусть начинается с символа
начинается с символа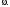 Тогда
Тогда где
где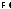 – формула. Так как
– формула. Так как – начало
– начало то
то также начинается с
также начинается с поэтому
поэтому где
где – формула. Очевидно,
– формула. Очевидно, – начало
– начало Значит, по предположению индукции
Значит, по предположению индукции Отсюда следует, что
Отсюда следует, что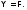 Наконец, разберём случай, когда
Наконец, разберём случай, когда начинается с левой скобки.Тогда
начинается с левой скобки.Тогда
 где
где – один из символов
– один из символов а
а и
и – формулы. Так как
– формулы. Так как
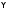 – начало
– начало то
то также начинается с левой скобки, а
значит,
также начинается с левой скобки, а
значит, где
где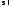
 а
а и
и –формулы.
Так как
–формулы.
Так как
 – начало
– начало то либо
то либо – начало
– начало либо
либо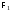 – начало
– начало
 В обоих случаях по предположению индукции
получаем
В обоих случаях по предположению индукции
получаем Но тогда
Но тогда и
и Отсюда следует, что
Отсюда следует, что
Теорема
1. Всякая
неатомарная формула
 единственным образом представима в
одном из следующих видов:
единственным образом представима в
одном из следующих видов:

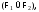
 где
где и
и – формулы.Доказательство.
Существование такого представления
следует из определения формулы. Надо
лишь доказать единственность. Понятно,
что если
– формулы.Доказательство.
Существование такого представления
следует из определения формулы. Надо
лишь доказать единственность. Понятно,
что если
 представима в виде
представима в виде то её нельзя представить в виде
то её нельзя представить в виде и надо лишь применить предположение
индукции к формуле
и надо лишь применить предположение
индукции к формуле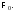 Пусть
Пусть представима в виде
представима в виде неоднозначно. Тогда
неоднозначно. Тогда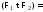
 Одна из формул
Одна из формул является началом другой. Значит, по
лемме 1
является началом другой. Значит, по
лемме 1 Но тогда
Но тогда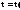 и
и Это доказывает единственность.
Это доказывает единственность.
Следствие.
Пусть
 – формула ИВ. Тогда с каждым вхождением
символа
– формула ИВ. Тогда с каждым вхождением
символа или символа
или символа в эту формулу однозначно связывается
вхождение в
в эту формулу однозначно связывается
вхождение в подформулы, начинающейся с этого символа.Доказательство.
Действительно, если в
подформулы, начинающейся с этого символа.Доказательство.
Действительно, если в
 есть символ
есть символ то при построении формулы
то при построении формулы ранее была построена формула
ранее была построена формула начинающаяся с этого символа, причём
начинающаяся с этого символа, причём – тоже формула. Формула
– тоже формула. Формула как раз и является подформулой,
начинающейся с данного вхождениясимвола
как раз и является подформулой,
начинающейся с данного вхождениясимвола
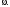 Единственность следует из леммы 1.
Аналогично разбираются случаи вхождения
в
Единственность следует из леммы 1.
Аналогично разбираются случаи вхождения
в символа (.
символа (.
