18. Аксиома выбора. Теорема Цермело.

Цепью называется линейно упорядоченное множество.

Пусть – частично упорядоченное множество и Г – его подмножество, являющееся цепью.Мажорантой (или верхней границей) цепи Г называется любой элемент такой, чтодля всех

Обозначим через множество всех мажорант цепи Г. Введём ещё одно обозначение. Пусть Г – цепь иПоложим

Аксиома выбора. Если – непустое множество, то в каждом его непустом подмножестве можно выбрать по одному элементу. Иными словами, существуетфункция выбора такая, чтопри любом непустом

1. Аксиома выбора (формулировку см. в начале раздела).

2. Лемма Цорна. Пусть – частично упорядоченное множество, в котором каждая цепь имеет мажоранту. Тогдаимеет хотя бы один максимальный элемент.

3. Теорема Цермело. На всяком множестве можно ввести отношение порядка, превращающее его во вполне упорядоченное множество.

_{Доказательство.} 1)A – множество, существует функция выбора такая, чтопри любом непустом _{2) назовем подмножество В отмеченным, если 1. В вполне упорядоченно каким-то отношением порядка. 2. 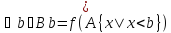. 3) Докажем, что для любых двух отмеченных множеств одно из них является начальным отрезком другого. МножестваB1 и B2. b1 = min B1, b2 = min B2. b1 = f(A), b2 = f(A). b1 = b2. b1’ = f(A\{b1}), b2’ = f(A\{b2}). b1’ = b2’. φ : нач.отрезок B1 -> нач.отрезок B2, рассмотрим такие отображения. φ(b1) = b1, φ(b1’) = b1’. Пусть φ(x) = x не для всех x. Берем первое несовпадение U= min(xᴄB1, | φ(x) != x ). U = f(A\C). φ(U) = f(A\C). U = φ(U) – противор.}

_{Значит из B1, B2 – одно – начальный отрезок другого.}

4. _{B* = U B(B - отмеченные). B* - вполне упорядоченное, b c B* b c B (сущ.отмеченн. B). b = f(A\{x| x<b}). C – непустое подмножество B*, C пересеч. B != пуст.мн-во. Min(C пересеч. B) = min(C ).}

5. _{Если B* = A, то доказано. Иначе возьмем a = f(A\B*). Новое B = B U {a}, но B* - самое большое отмеченное. |B|>|B*| - противоречие.}

19. Лемма Цорна.

Цепью называется линейно упорядоченное множество.

Пусть – частично упорядоченное множество и Г – его подмножество, являющееся цепью.Мажорантой (или верхней границей) цепи Г называется любой элемент такой, чтодля всех

Обозначим через множество всех мажорант цепи Г. Введём ещё одно обозначение. Пусть Г – цепь иПоложим

Аксиома выбора. Если – непустое множество, то в каждом его непустом подмножестве можно выбрать по одному элементу. Иными словами, существуетфункция выбора такая, чтопри любом непустом

1. Аксиома выбора (формулировку см. в начале раздела).

2. Лемма Цорна. Пусть – частично упорядоченное множество, в котором каждая цепь имеет мажоранту. Тогдаимеет хотя бы один максимальный элемент.

3. Теорема Цермело. На всяком множестве можно ввести отношение порядка, превращающее его во вполне упорядоченное множество.

Лемма Цорна

А – частично упорядоченно мн-во. Любая цепь в А имеет мажоранту(любой х, х не обязательно принадлежит Г. Тогда в А есть мах эл-т.

Док-во: f- ф-ия выбора. Цепь Г назовем отмеченной, если она вполне упорядочена и , гдеu|u>x , причем.

От противного: пусть нет мах эл-та. Тогда для любой цепи Г В(Г)- бесконечное мн-во.- отмеченная цепь,. Также как в теореме Цермело. Г1 начальный отрезок Г2 или наоборот. Г*=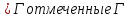- тоже отмеченная цепь. Объединение цепей не всегда цепь.отмеченный цепи,либо- начальный отрезоклибо наоборот, тогда- тоже цепь.Пусть, тогда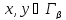=> сравнимы.

Г* - наиб. отмеченная цепь - имеет мажоранту по условию В(Г*).f(B(Г*))=.*- больше Г*. Противоречие.