
- •Правила вывода (здесь – какие-либо последовательности формул, возможно, пустые):
- •11. Теорема Шрёдера – Бернштейна.
- •Свойства эквивалентности множеств:
- •12. Счетные множества и их свойства.
- •Свойства счётных множеств:
- •13. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
- •Свойства множеств мощности континуума
- •14. Связь между счетными множествами и множествами мощности континуума.
- •15. Теорема Кантора о мощности множества всех подмножеств данного множества.
- •16. Эквиваленстность множеств(см.Ниже)
- •17. Вполне упорядоченные множества и их свойства.
- •Свойства вполне упорядоченных множеств:
- •18. Аксиома выбора. Теорема Цермело.
- •19. Лемма Цорна.
- •20. Ординальные числа и их свойства.
- •21. Кардинальные числа и их свойства.
- •22. Мощность множества АхА
- •23. Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •24. Аксиомы действительных чисел.
- •25. Модель, сигнатура. Формулы исчисления предикатов(логики первого порядка). Истинность формулы в данной модели.
- •26. Элиминация кванторов.
- •27. Фильтр. Центрированная система множеств.
- •28. Ультрафильтр. Характеризация ультрафильтров.
- •29. Ультрапроизведение моделей. Истинность формул на ультрапроизведении. Th. Лося.
- •30. Теорема Гёделя – Мальцева и следствие из нее.
- •31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.
- •32. Примитивно рекурсивные и рекурсивные функции.
- •33. Разрешимые множества и их свойства.
- •34. Перечислимые множества. Их связь с разрешимыми. Характеризация перечислимых множеств.
- •35. Существование перечислимого неразрешимого множества.
13. Несчестность множества действительных чисел. Свойства множеств мощности континуума.
Определение.
Множество
 называетсянесчётным,
если оно бесконечно и неэквивалентно
счётному множеству (т.е. его мощность
больше
называетсянесчётным,
если оно бесконечно и неэквивалентно
счётному множеству (т.е. его мощность
больше  ).
).
Теорема
2 (Кантор).
Множество
 несчётно.
несчётно.
Доказательство.
Каждое число
 имеет десятичную запись
имеет десятичную запись где
где При этом некоторые числа могут быть
записаны двумя способами, например,
При этом некоторые числа могут быть
записаны двумя способами, например, Из этих двух записей выберем первую,
т.е. запретим ситуацию, когда в десятичной
записи числа, начиная с некоторого
момента, идут одни девятки. Исключением
сделаем лишь число
Из этих двух записей выберем первую,
т.е. запретим ситуацию, когда в десятичной
записи числа, начиная с некоторого
момента, идут одни девятки. Исключением
сделаем лишь число
Предположим,
что множество
 счётно. Тогда
счётно. Тогда


Представим
 в виде десятичной дроби:
в виде десятичной дроби:

Теперь
построим число
 следующим образом. Пусть
следующим образом. Пусть любая цифра, отличная от
любая цифра, отличная от и 9,
и 9, любая цифра, отличная от
любая цифра, отличная от и 9, и вообще,
и 9, и вообще,
 Положим
Положим Тогда
Тогда при всех
при всех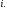 Так как
Так как ,
мы получили противоречие с равенством
,
мы получили противоречие с равенством Теорема доказана.
Теорема доказана.
Замечание. Приведённый здесь метод доказательства называется диагональным методом Кантора.
Определение.
Мощность множества чисел отрезка
 называетсямощностью
континуума
и обозначается с.
называетсямощностью
континуума
и обозначается с.
Очевидно,
с

Свойства множеств мощности континуума
1)
с
+ с
= с;
2) с
с
= с;
3) с
+  = с
= с
 = с.
= с.
Доказательство.
Докажем вначале свойство 2), т.е. тот
факт, что “квадрат
содержит столько же точек, сколько
отрезок”.
Очевидно,
 с.
Поэтому возьмём
с.
Поэтому возьмём
 Надо доказать, что
Надо доказать, что с.
Ввиду теоремы Шрёдера – Бернштейна нам
достаточно вложить
с.
Ввиду теоремы Шрёдера – Бернштейна нам
достаточно вложить
 в
в и вложить
и вложить в
в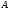 Вложение
Вложение в
в для любого непустого множества
для любого непустого множества осуществляется очень просто:
осуществляется очень просто: где
где – фиксированный элемент из
– фиксированный элемент из Теперь вложим множество
Теперь вложим множество в множество
в множество Пусть
Пусть Тогда
Тогда где
где Запишем
Запишем и
и в виде бесконечных десятичных дробей:
в виде бесконечных десятичных дробей:
 (как обычно, мы запрещаем дроби вида
(как обычно, мы запрещаем дроби вида ). Рассмотрим отображение
). Рассмотрим отображение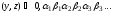 Нетрудно проверить, что оно является
вложением множества
Нетрудно проверить, что оно является
вложением множества в
в
Свойство 1) можно доказать, используя 2) и теорему Шрёдера – Бернштейна. А именно, ясно, что множество мощности с вкладывается в множество мощности с + с. Далее, с + с – это мощность объединения двух отрезков. Оно вкладывается в квадрат, а квадрат вкладывается в отрезок.
Свойство 3) доказывается аналогичными рассуждениями. Доказательство предоставляется читателю.
14. Связь между счетными множествами и множествами мощности континуума.
Связь между счётными множествами и множествами мощности континуума даёт следующая теорема.
Теорема.

Доказательство.
Теорему можно переформулировать так:
множество всех подмножеств счётного
множества имеет мощность континуума.
Ввиду теоремы Шрёдера – Бернштейна нам
достаточно построить вложения
 и
и Каждый элемент
Каждый элемент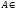
 можно задать последовательностью из
0 и 1; а именно,
можно задать последовательностью из
0 и 1; а именно, где
где Вложение
Вложение имеет следующий вид::
имеет следующий вид::
Теперь
вложим
 в
в .
Элементы из
.
Элементы из представим
в виде бесконечных двоичных дробей,
запретив для однозначности записи вида
представим
в виде бесконечных двоичных дробей,
запретив для однозначности записи вида для всех чисел, кроме
для всех чисел, кроме Вложение
Вложение в
в осуществим так:
осуществим так:
 где
где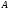 состоит из тех
состоит из тех N,
у которых
N,
у которых

15. Теорема Кантора о мощности множества всех подмножеств данного множества.
Теорема
6 (теорема Кантора).
Для любого множества
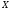

Доказательство.
Вложение
 осуществляется просто:
осуществляется просто: Нам осталось доказать, что не существует
взаимно однозначного соответствия
между множествами
Нам осталось доказать, что не существует
взаимно однозначного соответствия
между множествами и
и Предположим, что существует взаимно
однозначное соответствие
Предположим, что существует взаимно
однозначное соответствие т.е. каждому элементу
т.е. каждому элементу ставится в соответствие подмножество
ставится в соответствие подмножество причём каждое подмножество
причём каждое подмножество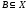 представимо в виде
представимо в виде при некотором
при некотором По условию
По условию при некотором
при некотором значит,
значит, Далее,
Далее, при некотором
при некотором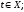 в этом случае
в этом случае Построим подмножество
Построим подмножество множества
множества полагая
полагая Так как
Так как то
то при некотором
при некотором Выясним, верно ли соотношение
Выясним, верно ли соотношение Имеем:
Имеем:
а)
если
 то
то по определению множества
по определению множества получаем:
получаем:
б)
если
 то
то по определению множества
по определению множества получаем:
получаем: что невозможно. Мы получили противоречие.
Теорема доказана.
что невозможно. Мы получили противоречие.
Теорема доказана.
Из
теоремы Кантора следует, что среди
множеств нет наибольшего по мощности,
так как, каково бы ни было множество
 множество
множество имеет ещё большую мощность. В частности,
имеет ещё большую мощность. В частности, <
...
<
...
