30. Теорема Гёделя – Мальцева и следствие из нее.

Предложением мы будем называть замкнутую формулу, т.е. формулу, не содержащую свободных переменных. Теорией будем называть совокупность предложений (конечную или бесконечную) одной сигнатуры. Будем говорить, что теория имеет модель если все предложения теорииистинны на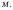Далее, если– теория, а Ф – замкнутая формула УИП, то мы пишемесли Ф истинна на любой модели теориит.е. Ф истинна на любой модели, на которой истинны все формулы из

Теорема 5 (теорема компактности Гёделя – Мальцева). Если каждое конечное подмножество имеет модель, то теорияимеет модель.

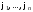Доказательство. Пусть – множество всех конечных подмножеств множестваи– модель дляДля формулыпустьистинна наПроверим, что– центрированная система подмножеств множестваДействительно, рассмотрим конечное подмножествоТогдаЗначит, формулыистинны на моделиследовательно,Таким образом,Мы показали, что– центрированная система. По теореме 1 и теореме 2 эту систему можно вложить в некоторый ультрафильтрРассмотрим ультрапроизведениеПустьТогдаистинна на всехгдеНозначит, по теореме Формуладанной сигнатуры истинна на наборев том и только в том случае, если)истинна на ультрапроизведенииТаким образом,G является моделью для

Для доказательства неаксиоматизируемости некоторых классов алгебраических систем часто используется следствие из теоремы компактности, которое мы сейчас приведём.

Следствие. Пусть – множество предложений логики первого порядка иТогда существует конечное подмножествотакое, что

Доказательство. Предположим противное, т.е. что для любого конечногоТогда для каждого конечногосуществует модель, для которой предложениеистинно. По теореме компактности существует модель, в которой все предложения изT и предложение истинны. Но тогдавопреки условию.

31. Машины Тьюринга и вычислимые функции. Понятие алгоритма. Тезис Чёрча.

Машина Тьюринга так же, как и конечный автомат, является дискретным устройством преобразования информации. Приведём её точное определение, а затем интерпретацию её работы.

Машиной Тьюринга называется частичное отображение (множество состояний)

Где обозначает “лево”, “право”. Тот факт, что отображениечастичное, означает, чтоможет быть определено не для всех наборов аргументов. Машина Тьюрингаработает с бесконечной в обе стороны лентой, разбитой на ячейки, в каждой из которых написан один из символов 0, 1. Считывающая головка машины обозревает в каждый момент времени одну из ячеек и за один такт, сменяющий два последовательных момента времени, может перемещаться влево или вправо. Машина Тьюринга в каждый момент времени находится в одном из состоянийа в следующий момент времени переходит в другое состояние или остаётся в том же. Кроме того, машина может изменять символ, стоящий в обозреваемой ячейке. Все эти преобразования – изменение состояния, информация на ленте, направление движения полностью определяются отображениемА именно, еслито в случае, когда машина находится в состоянииа на обозреваемой в данный момент ячейке написан символмашина должна записать в эту ячейкувместоперейти в состояниеи сдвинуться на одну ячейкувлево. Например, равенство означает, что, находясь в состояниии обозревая ячейку, в которой написан символ 1, машина должна сохранить в этой ячейке символ 1, сдвинуться вправо и перейти в состояниеЕсли жене определено, то машина, находясь в состояниии обозревая ячейку с символомпрекращает работу, не изменяя своего состояния, информации на ленте и никуда не сдвигаясь.

Более удобна запись программы, которая заключает в себе всю информацию о работе машины (таким образом, задания машины с помощью отображения и с помощью программы эквивалентны между собой). Опишем составление программы. Для каждого равенства вида гденомера состояний,направление движения, асимволы на ленте, запишем строкуи назовём еёкомандой. Совокупность всех команд – это и есть программа. Если не определено, то в программе нет ни одной команды, начинающейся сКроме того, для любыхв программе есть не более одной команды, начинающейся с

Будем говорить, что машина Тьюринга вычисляет функцию если для любого наборанатуральных чисел машинанаходясь в состояниии обозревая крайнюю левую единицу в(причём [xi]=i+1 единиц, как и значение f )останавливается в том и только в том случае, когда значение определено, и в конце работы ленте должно быть записано ...00..., а считывающая головка машины должна стоять напротив крайней левой единицы.

Таким образом, если, например, то мы должны иметь

а если не существует, то машина, запущенная на ленте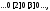должна работать бесконечно долго (при условии, что начальное состояниеа обозреваемая в начальный момент времени ячейка – крайняя левая единица.

Если информация на ленте не имеет вид или начальное состояние неили обозреваемая ячейка – не крайняя левая единица, то поведение машины может быть каким угодно.

Под алгоритмом понимается жёсткое правило, следование которому и выполнение всех его предписаний приводит к решению задачи. Конечно, эту фразу нельзя считать определением алгоритма.

Тезис Чёрча. Понятие алгоритма, или вычислимости некоторым механическим устройством, совпадает с понятием вычислимости на машинах Тьюринга (а значит, с понятием рекурсивной функции).