
- •Генценовское ив. Правила вывода. Секвенции. Доказательства. Допустимые правила.
- •Допустимые правила:
- •Интерпретация ив. Истинность формул и секвенций на наборе переменных. Тождественная истинность.
- •Либо при некотором либо
- •Теорема о полноте ив.
- •Разрешимость классического исчисления высказываний.
- •Понятие об интуиционизме и конструктивизме в логике.
- •Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •Свойства счётных множеств:
- •Несчётность множества действительных чисел. Свойства множеств мощности континуума.
- •Связь между счётными множествами и множествами мощности континуума.
- •Теорема Кантора о мощности множества всех подмножеств данного множества.
- •Эквивалентность множеств и
- •Вполне упорядоченные множества и их свойства.
- •Ординальные числа и их свойства..
- •Кардинальные числа и их свойства.
- •Мощность множества
- •Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •Логические связки:
- •Ультрафильтр. Характеризация ультрафильтров.
- •Ультрапроизведение моделей. Истинность формул на ультрапроизведении. Теорема Лося.
- •Теорема Гёделя – Мальцева и следствие из неё.
- •Теорема Лёвенгейма-Скулема о повышении мощности
- •Простейшие функции о s I
- •Является вычислимой.
- •Универсальные вычислимые функции.
- •Существование перечислимого неразрешимого множества.
- •Алгоритмически неразрешимые задачи. Алгоритмическая неразрешимость проблемы остановки машины Тьюринга.
-
Интуиционистское ив. Недоказуемость закона исключённого третьего.
В интуиционистской
логике двойное отрицание неэквивалентно
отсутствию отрицания. Однако, тройное
отрицание эквивалентно однократному.
Действительно, в доказательстве формулы
![]() можно сразу вместо
можно сразу вместо
![]() взять
взять
![]() и мы получим:
и мы получим:
![]() Возьмём в формуле
Возьмём в формуле
![]() вместо
вместо
![]() формулу
формулу
![]() Тогда получим:
Тогда получим:
![]() Так как
Так как
![]() уже доказано, то по modus
ponens получаем:
уже доказано, то по modus
ponens получаем:
![]()
Докажем
теперь невыводимость формулы
![]() (закона
исключённого третьего)
в интуиционистской логике. Рассмотрим
трёхзначное множество значений истинности
(закона
исключённого третьего)
в интуиционистской логике. Рассмотрим
трёхзначное множество значений истинности
![]() в котором 0 интерпретируется как ложь
(Л), 1 – как истина (И),
в котором 0 интерпретируется как ложь
(Л), 1 – как истина (И),
![]() – как неопределённость (Н). Определим
конъюнкцию и дизъюнкцию обычным способом:
– как неопределённость (Н). Определим
конъюнкцию и дизъюнкцию обычным способом:
![]()
![]() отрицание:
отрицание:
![]()
![]()
![]() Импликация определяется так:
Импликация определяется так:

Можно
проверить, что аксиомы гильбертова
исчисления (1)-(10) являются тождественно
истинными в трёхзначной логике, т.е. при
любом присвоении буквам
![]() значений из множества
значений из множества
![]() формула оказывается равной 1. Кроме
того, правило modus
ponens
сохраняет тождественную истинность.
Значит, все выводимые в ИИВ формулы
тождественно истинны (и трёхзначной
логике). Однако, формула
формула оказывается равной 1. Кроме
того, правило modus
ponens
сохраняет тождественную истинность.
Значит, все выводимые в ИИВ формулы
тождественно истинны (и трёхзначной
логике). Однако, формула
![]() тождественно истинной не является, так
как при
тождественно истинной не является, так
как при
![]() Н
Н
![]()
![]() Значит, формула
Значит, формула
![]() невыводима в ИИВ.
невыводима в ИИВ.
Замечание.
Существуют тождественно истинные, но
невыводимые в ИИВ формулы. Например,
![]()
![]()
-
Эквивалентные множества и их свойства. Теорема Шрёдера – Бернштейна.
Определение.
Множества
![]() и
и
![]() называются эквивалентными
(или равномощными),
если существует взаимно однозначное
отображение множества
называются эквивалентными
(или равномощными),
если существует взаимно однозначное
отображение множества
![]() на множество
на множество
![]()
Для
эквивалентных множеств мы будем писать
![]() или
или
![]()
Свойства эквивалентности множеств
-

-
если
 то
то
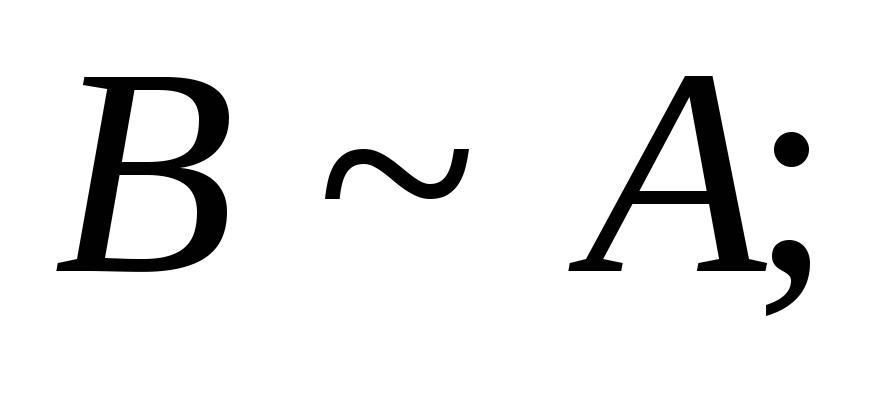
-
если
 а
а
 то
то

Доказательство.
1) Тождественное отображение
![]()
![]() является взаимно однозначным; 2) если
является взаимно однозначным; 2) если
![]() взаимно однозначно, то
взаимно однозначно, то
![]() – тоже; 3) если
– тоже; 3) если
![]() и
и
![]() – взаимно однозначные отображения,
то
– взаимно однозначные отображения,
то
![]() (
(![]() – взаимно однозначное отображение.
– взаимно однозначное отображение.
Замечание. Нельзя назвать “эквивалентность множеств” отношением эквивалентности, потому что непонятно, на каком множестве рассматривается это отношение (такого понятия, как “множество всех множеств”, не существует).
Определение.
Мощностью
множества
![]() называется совокупность всех множеств,
эквивалентных множеству
называется совокупность всех множеств,
эквивалентных множеству
![]()
Мощность
множества
![]() обозначается
обозначается
![]()
Теперь нам надо научиться сравнивать множества по мощности.
Определение.
Говорят, что мощность множества
![]() не превосходит
мощности множества
не превосходит
мощности множества
![]() (записываем:
(записываем:
![]() если существует вложение
множества
если существует вложение
множества
![]() в множество
в множество
![]() Если существует вложение
Если существует вложение
![]() в
в
![]() но не существует взаимно однозначного
отображения
но не существует взаимно однозначного
отображения
![]() на
на
![]() то мы говорим, что мощность множества
то мы говорим, что мощность множества
![]() строго меньше
мощности множества
строго меньше
мощности множества
![]() и пишем
и пишем
![]()
Очевидны следующие свойства:
Гораздо
менее очевидным является следующее
свойство, называемое теоремой Шрёдера
– Бернштейна:
![]()
![]()
![]()
Теорема
1 (теорема Шрёдера – Бернштейна).
Если существуют вложения
![]() и
и
![]() то существует взаимно однозначное
отображение
то существует взаимно однозначное
отображение
![]()
Доказательство.
Положим
![]()
![]() Пусть
Пусть
![]()
![]()
![]()
![]() и вообще
и вообще
![]()
![]() Мы имеем:
Мы имеем:
 где
где
![]() (1)
(1)
 где
где
![]() (2) Очевидно,
(2) Очевидно,
![]() взаимно однозначно отображает
взаимно однозначно отображает
![]() на
на
![]() поэтому существует
поэтому существует
![]() также взаимно однозначное. Проверим,
что
также взаимно однозначное. Проверим,
что
![]() взаимно однозначно отображает
взаимно однозначно отображает
![]() на
на
![]() Действительно, пусть
Действительно, пусть
![]() Так как
Так как
![]() то
то
![]()
![]() Следовательно,
Следовательно,
![]() Пусть
Пусть
![]() Так как
Так как
![]() и
и
![]() то
то
![]() для некоторого
для некоторого
![]() Так как
Так как
![]() – вложение, то
– вложение, то
![]() Следовательно,
Следовательно,
![]()
![]() Таким образом,
Таким образом,
![]() взаимно однозначно. Кроме того,
взаимно однозначно. Кроме того,
![]() взаимно однозначно отображает
взаимно однозначно отображает
![]() на
на
![]()
![]() на
на
![]() и т.д., а
и т.д., а
![]() взаимно однозначно отображает
взаимно однозначно отображает
![]() на
на
![]()
![]() на
на
![]() и т.д. Пользуясь соотношениями (1) и (2),
нетрудно убедиться в том, что отображение
и т.д. Пользуясь соотношениями (1) и (2),
нетрудно убедиться в том, что отображение
![]() определённое правилом
определённое правилом

является взаимно однозначным. Теорема доказана.
Эта
теорема, наряду с теоретическим, имеет
большое практическое значение. Она
позволяет доказывать эквивалентность
множеств
![]() и
и
![]() не строя взаимно однозначного отображения
не строя взаимно однозначного отображения
![]() а построив лишь вложения
а построив лишь вложения
![]() и
и
![]()
-
Счётные множества и их свойства.
Определение.
Множество
![]() называется счётным,
если
называется счётным,
если
![]() N.
N.
Например,
счётным является множество 2N
чётных натуральных чисел. Действительно,
отображение
![]() задаёт взаимно однозначное соответствие
между множествами N
и 2N.
задаёт взаимно однозначное соответствие
между множествами N
и 2N.
