1. символы из множеств и

2. алфавит предметных переменных; их мы будем, как правило, обозначать маленькими латинскими буквами (преимущественно из второй половины алфавита) с индексами или без, т.е. алфавит как правило, будет предполагаться счётным;

3. Логические связки:

4. служебные символы: “,”, “(”, “)” (запятая, левая и правая скобки).

Терм определяется индуктивно:

1. предметная переменная – терм;

2. если – термы и – символ п-арной операции, то – терм.

Формула логики первого порядка и множество свободных переменных формулы определяются индуктивно:

1. если – термы и – символ п-местного отношения, то – формула (такие формулы называются атомарными); свободными переменными формулы. называются предметные переменные, входящие хотя бы в один из термов

2. если – формула, то – формула и

3. если и – формулы и ни одна из предметных переменных не входит свободно в одну из этих формул, а несвободно в другую, то – формулы и

4. если – формула и – предметная переменная, которая либо не входит в формулу либо входит в неё свободно, то и – формулы и

Формула называется замкнутой, если она не содержит свободных переменных, т.е. Замкнутую формулу можно назвать высказыванием. Незамкнутые формулы являются предикатами.

Пусть – модель, где – носитель, – сигнатура и – формула УИП со свободными переменными Истинность или ложность этой формулы зависит от того, какие значения мы придадим переменным Назовём оценкой отображение (смысл её состоит в том, что мы каждой предметной переменной присваиваем какое-то значение из множества Определим значение истинности формулы на оценке Истину мы будем обозначать буквой И, а ложь – буквой Л. Определение построим индукцией по длине формулы. Положим ... ,

1. Если – атомарная формула, где – термы, то в том и только том случае, если

2. если имеет вид или то истинность или ложность высказывания определяется по обычным правилам;

3. если то в том и только том случае, если при всех

4. если то в том и только том случае, если при каком-нибудь

27. Элиминация кванторов.

В некоторых моделях для всякой формулы УИП, содержащей кванторы, существует эквивалентная ей формула без кванторов. В этом случае мы будем говорить, что модель допускает элиминацию кванторов.

Теорема. Модель где = – отношение равенства, – унарная операция и 0 – нульарная операция, допускает элиминацию кванторов.

Доказательство. Индукция по количеству кванторов в формуле. От квантора в любой формуле можно избавиться, заменив формулу на эквивалентную ей формулу Таким образом, нам достаточно доказать, что формула где не содержит кванторов, имеет эквивалентную ей бескванторную формулу. Формула получается из атомарных формул с помощью логических связок. Атомарные формулы, содержащие переменную имеют вид или или

Формула первого типа либо тождественно истинна, либо тождественно ложна, поэтому её можно заменить на эквивалентную формулу, не содержащую или Формулы второго и третьего типа можно кратко записать в виде где или ( – константа, не обязательно положительная), Рассмотрим формулу

Очевидно, что если формула истинна на каком-либо наборе то формула также истинна на этом наборе. Обратное в общем случае неверно, так как может быть сделана истинной, когда для некоторого отличного от всех Но тогда все атомарные формулы ложны. Заменим каждую из этих формул на какую-нибудь тождественно ложную формулу и обозначим полученную формулу через Тогда формула будет эквивалентна формуле

28. Фильтр. Центрированная система множеств.

Фильтром на множестве называется совокупность F подмножеств множества обладающая свойствами:

1. F;

2. F, F;

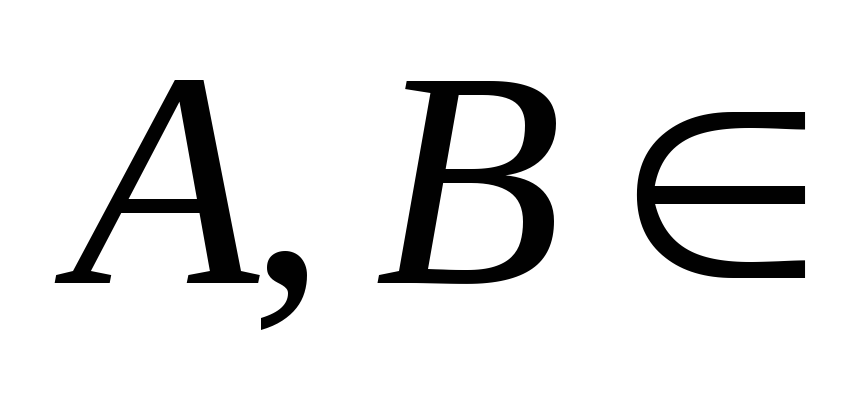3. FF.

Пусть – совокупность подмножеств множества Она называется центрированной системой подмножеств (иногда говорят: обладает свойством конечных пересечений), если пересечение любого конечного числа множеств из непусто, т.е.

Теорема 1. Всякая центрированная система подмножеств вкладывается в фильтр.

Доказательство. Пусть – центрированная система подмножеств множества Обозначим через F совокупность таких подмножеств множества что для некоторых Проверим, что F – фильтр. Из определения системы следует, что при всех F. Значит, F. Пусть F и Так как при некоторых то также Значит, F. Наконец, пусть F. Тогда при некоторых Следовательно, а значит, F.