
- •Генценовское ив. Правила вывода. Секвенции. Доказательства. Допустимые правила.
- •Допустимые правила:
- •Интерпретация ив. Истинность формул и секвенций на наборе переменных. Тождественная истинность.
- •Либо при некотором либо
- •Теорема о полноте ив.
- •Разрешимость классического исчисления высказываний.
- •Понятие об интуиционизме и конструктивизме в логике.
- •Интуиционистское ив. Недоказуемость закона исключённого третьего.
- •Свойства счётных множеств:
- •Несчётность множества действительных чисел. Свойства множеств мощности континуума.
- •Связь между счётными множествами и множествами мощности континуума.
- •Теорема Кантора о мощности множества всех подмножеств данного множества.
- •Эквивалентность множеств и
- •Вполне упорядоченные множества и их свойства.
- •Ординальные числа и их свойства..
- •Кардинальные числа и их свойства.
- •Мощность множества
- •Аксиомы Пеано натуральных чисел. Коммутативность сложения.
- •Логические связки:
- •Ультрафильтр. Характеризация ультрафильтров.
- •Ультрапроизведение моделей. Истинность формул на ультрапроизведении. Теорема Лося.
- •Теорема Гёделя – Мальцева и следствие из неё.
- •Теорема Лёвенгейма-Скулема о повышении мощности
- •Простейшие функции о s I
- •Является вычислимой.
- •Универсальные вычислимые функции.
- •Существование перечислимого неразрешимого множества.
- •Алгоритмически неразрешимые задачи. Алгоритмическая неразрешимость проблемы остановки машины Тьюринга.
-
Исчисление высказываний. Формулы. Теорема о единственности представления формулы ИВ в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.
Алфавит ИВ содержит следующие символы:
-
пропозициональные переменные
 – они обозначают элементарные
высказывания – это “кирпичики”, из
которых будут формироваться другие,
более сложные высказывания;
– они обозначают элементарные
высказывания – это “кирпичики”, из
которых будут формироваться другие,
более сложные высказывания; -
логические связки:

-
служебные символы: “(“, “)”, “,” (левая скобка, правая скобка, запятая);
-
символ

Формула ИВ определяется индуктивно по следующей схеме:
-
атомарные формулы (простейшие) – это пропозициональные переменные;
-
если
 и
и
 – формулы, то
– формулы, то



 – формулы.
– формулы.
Пусть
дано слово
![]() в алфавите
в алфавите
![]() Подсловом
этого слова мы называем всякое слово
вида
Подсловом
этого слова мы называем всякое слово
вида
![]() где
где
![]() началом
слова
началом
слова
![]() называется подслово вида
называется подслово вида
![]()
![]() Слово, в котором нет ни одной буквы,
называется пустым
словом и
обозначается символом
Слово, в котором нет ни одной буквы,
называется пустым
словом и
обозначается символом
![]() Пустое слово является подсловом любого
слова. Подформулой
формулы
Пустое слово является подсловом любого
слова. Подформулой
формулы
![]() мы будем называть подслово слова
мы будем называть подслово слова
![]() которое само является формулой.
которое само является формулой.
Лемма
1. Если
![]() и
и
![]() – формулы и
– формулы и
![]() – начало
– начало
![]() то
то
![]()
Теорема
1. Всякая
неатомарная формула
![]() единственным образом представима в
одном из следующих видов:
единственным образом представима в
одном из следующих видов:
![]()
![]()
![]()
![]() где
где
![]() и
и
![]() – формулы.
– формулы.
Доказательство.
Существование такого представления
следует из определения формулы. Надо
лишь доказать единственность. Понятно,
что если
![]() представима в виде
представима в виде
![]() то её нельзя представить в виде
то её нельзя представить в виде
![]() и надо лишь применить предположение
индукции к формуле
и надо лишь применить предположение
индукции к формуле
![]() Пусть
Пусть
![]() представима в виде
представима в виде
![]() неоднозначно. Тогда
неоднозначно. Тогда
![]()
![]() Одна из формул
Одна из формул
![]() является началом другой. Значит, по
лемме 1
является началом другой. Значит, по
лемме 1
![]() Но тогда
Но тогда
![]() и
и
![]() Это доказывает единственность.
Это доказывает единственность.
-
Генценовское ив. Правила вывода. Секвенции. Доказательства. Допустимые правила.
Секвенцияяи мы будем называть записи одного из следующих видов:
Здесь
![]() – формулы ИВ, знак
– формулы ИВ, знак
![]() читается “выводится. Секвенция (1)
расшифровывается так: из формул
читается “выводится. Секвенция (1)
расшифровывается так: из формул
![]() выводится формула
выводится формула
![]() Секвенция (2) означает, что совокупность
формул
Секвенция (2) означает, что совокупность
формул
![]() противоречива. Секвенция (3) означает,
что формула
противоречива. Секвенция (3) означает,
что формула
![]() выводима. Секвенцию (4) мы комментировать
не будем. Она не будет иметь доказательства
ни при каких обстоятельствах.
выводима. Секвенцию (4) мы комментировать
не будем. Она не будет иметь доказательства
ни при каких обстоятельствах.
Аксиомами
ИВ
называются секвенции вида
![]() где
где
![]() – формула (не обязательно атомарная).
Доказательства
осуществляются
на основе правил
вывода,
список которых мы приводим.
– формула (не обязательно атомарная).
Доказательства
осуществляются
на основе правил
вывода,
список которых мы приводим.
Правила вывода <…>
Доказательством Называется последовательность секвенций
![]()
где
каждое
![]() – либо аксиома, либо получается из
секвенций
– либо аксиома, либо получается из
секвенций
![]() с помощью правил вывода. Правило вывода
применяется следующим образом: если
секвенции, стоящие в числителе, уже
встречались в доказательстве, то на
любом дальнейшем шаге доказательства
мы можем написать секвенцию, стоящую в
знаменателе.
с помощью правил вывода. Правило вывода
применяется следующим образом: если
секвенции, стоящие в числителе, уже
встречались в доказательстве, то на
любом дальнейшем шаге доказательства
мы можем написать секвенцию, стоящую в
знаменателе.
Допустимые правила:
-
а)


б)
в)

з)

г)

и)

д)

к)

е)
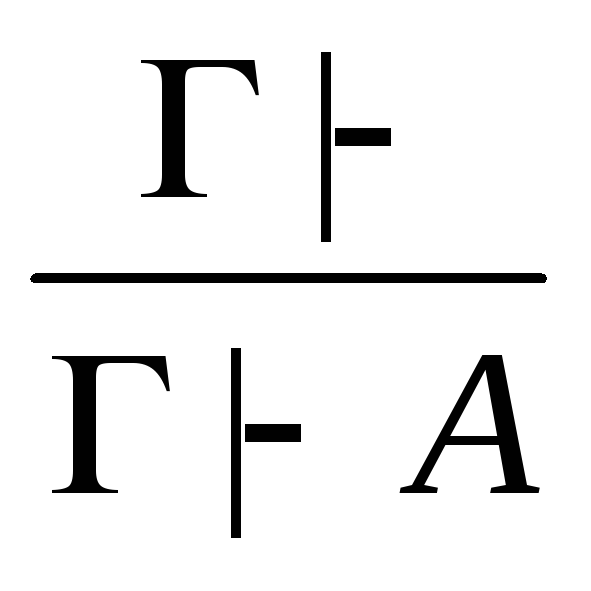
л)

ж)

м)
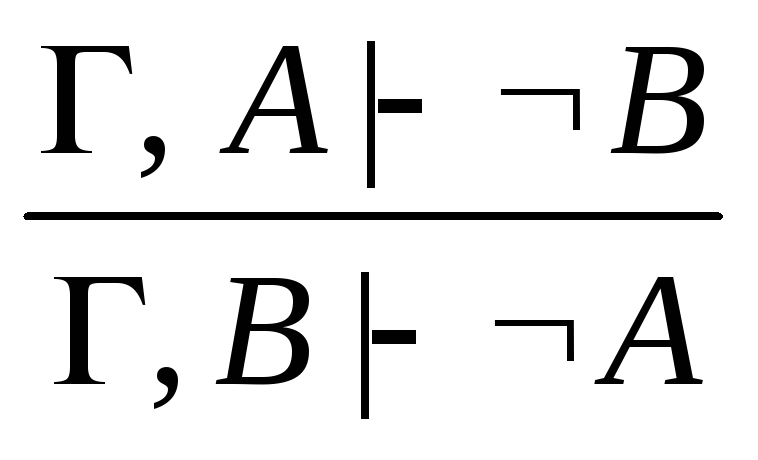
-
Доказательство секвенций
 и
и

Лемма
4. Для любой
формулы
![]() доказуема секвенция
доказуема секвенция
![]()
Доказательство.
-
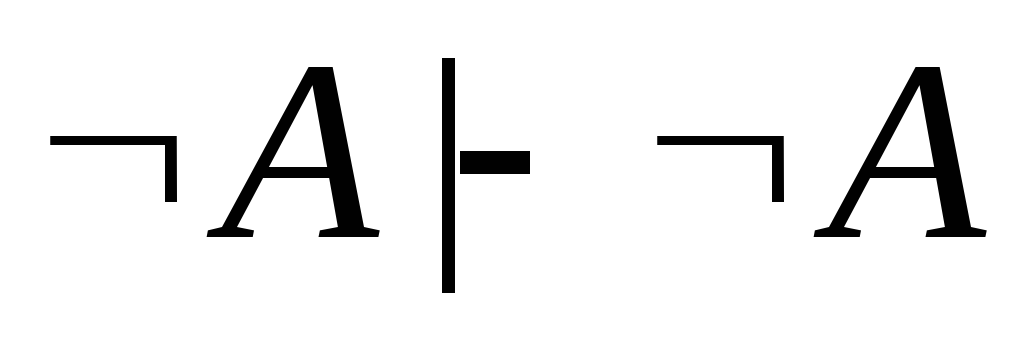 (аксиома);
(аксиома); -
 (из
(1) по правилу 5);
(из
(1) по правилу 5); -
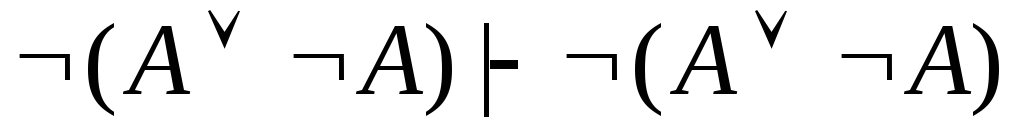 (аксиома);
(аксиома); -
 (из
(2) по правилу 12);
(из
(2) по правилу 12); -
 (из
(3) по правилам 11, 12);
(из
(3) по правилам 11, 12); -
 (из
(4) и (5) по правилу 10);
(из
(4) и (5) по правилу 10); -
 (из
(6) по правилам 9, 11);
(из
(6) по правилам 9, 11); -
 (из
(7) по правилу 4);
(из
(7) по правилу 4); -
 (из
(3) и (8) по правилу 10);
(из
(3) и (8) по правилу 10); -
 (из
(9) по правилу 9).
(из
(9) по правилу 9).
Лемма
5. Для любой
формулы
![]() доказуема секвенция
доказуема секвенция
![]()
Доказательство.
-
 (аксиома);
(аксиома); -
 (из
(1) по правилу 2);
(из
(1) по правилу 2); -
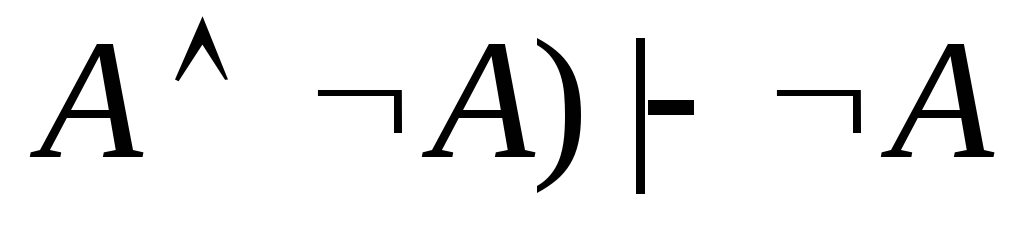 (из
(1) по правилу 3);
(из
(1) по правилу 3); -
 (из
(2) и (3) по правилу 10).
(из
(2) и (3) по правилу 10).
-
Эквивалентные формулы. Приведение формулы к нормальному виду.
Две формулы
![]() и
и
![]() называются эквивалентными
(обозначается:
называются эквивалентными
(обозначается:
![]() если доказуемы секвенции
если доказуемы секвенции
![]() и
и
![]()
Предложение
1. Отношение
![]() является отношением эквивалентности.
является отношением эквивалентности.
Доказательство.
Рефлексивность и симметричность
отношения
![]() очевидны. Докажем транзитивность. Пусть
очевидны. Докажем транзитивность. Пусть
![]() и
и
![]() Тогда
Тогда
![]()
![]()
![]()
![]() Так как
Так как
![]() и
и
![]() то по правилу
то по правилу
![]()
![]() Аналогично получаем
Аналогично получаем
![]() Таким образом,
Таким образом,
![]()
Замечание. Впоследствии мы докажем, что эквивалентность формул означает, что эти формулы совпадают как булевы функции, у которых аргументами являются атомарные формулы. Но это будет сделано лишь после достаточного развития теории.
Предложение
2. Если
![]() то для любой конечной последовательности
формул
то для любой конечной последовательности
формул
![]() доказуемость секвенции
доказуемость секвенции
![]() равносильна доказуемости секвенции
равносильна доказуемости секвенции
![]()
Теорема
1 (о
замене).
Если
![]() и
и
![]() то
то
![]()
![]()
![]()
![]()
Следствием этой теоремы
является тот факт, что если
![]() то любое вхождение формулы
то любое вхождение формулы
![]() в более сложную формулу
в более сложную формулу
![]() может быть заменено на формулу
может быть заменено на формулу
![]() причём новая формула будет эквивалентна
формуле
причём новая формула будет эквивалентна
формуле
![]() Доказательство осуществляется индукцией
по длине формулы
Доказательство осуществляется индукцией
по длине формулы
![]() К
К
Положим
 Пусть
Пусть
![]() – атомарные формулы. Выражение вида
– атомарные формулы. Выражение вида
![]() будем называть элементарной
дизъюнкцией,
если слагаемые в этом выражении все
разные. При этом, вообще говоря, формулы
будем называть элементарной
дизъюнкцией,
если слагаемые в этом выражении все
разные. При этом, вообще говоря, формулы
![]() не обязательно различные
не обязательно различные
Теорема
2. Для всякой
формулы
![]() рассматриваемой как выражение от
атомарных формул
рассматриваемой как выражение от
атомарных формул
![]() существует формула
существует формула
![]() такая, что
такая, что
![]() и
и
![]()
![]()
где каждая скобка является элементарной дизъюнкцией.
Доказательство.
Вначале избавимся в формуле
![]() от знака импликации
от знака импликации
![]() используя эквивалентность
используя эквивалентность
![]() Далее, пользуясь законами де-Моргана
Далее, пользуясь законами де-Моргана
![]()
![]() а также законом двойного отрицания
а также законом двойного отрицания
![]() мы сможем добиться того, чтобы знаки
отрицания
мы сможем добиться того, чтобы знаки
отрицания
![]() стояли только при атомарных формулах.
Затем, используя дистрибутивность
стояли только при атомарных формулах.
Затем, используя дистрибутивность
![]() мы сможем сделать так, чтобы внешним
действием была конъюнкция, т.е. получить
выражение вида
мы сможем сделать так, чтобы внешним
действием была конъюнкция, т.е. получить
выражение вида
![]() Наконец, благодаря эквивалентностям
Наконец, благодаря эквивалентностям
![]()
![]() мы можем привести подобные члены, после
чего каждая скобка в
мы можем привести подобные члены, после
чего каждая скобка в
![]() действительно будет элементарной
дизъюнкцией.
действительно будет элементарной
дизъюнкцией.
