1. Исчисление высказываний. Формулы. Теорема о единственности представления формулы ИВ в виде конъюнкции, дизъюнкции, отрицания или импликации других высказываний.

Алфавит ИВ содержит следующие символы:

1. пропозициональные переменные – они обозначают элементарные высказывания – это “кирпичики”, из которых будут формироваться другие, более сложные высказывания;

2. логические связки:

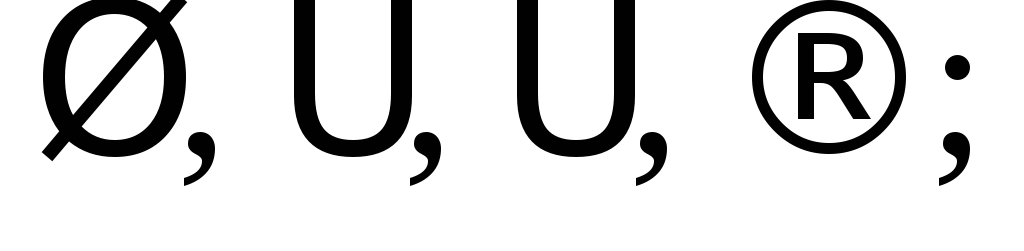
3. служебные символы: “(“, “)”, “,” (левая скобка, правая скобка, запятая);

4. символ

Формула ИВ (высказывание) определяется индуктивно по следующей схеме:

1. атомарные формулы (простейшие) – это пропозициональные переменные;

2. если и– формулы, то– формулы.

Итак, формулами ИВ называются только те слова, записанные в алфавите ИВ, которые получаются по вышеприведённой схеме. Например, если – пропозициональные переменные, то– формулы, а– не формулы.

Пусть дано слово в алфавитеПодсловом этого слова мы называем всякое слово вида гденачалом слова называется подслово видаСлово, в котором нет ни одной буквы, называетсяпустым словом и обозначается символом Пустое слово является подсловом любого слова.Подформулой формулы мы будем называть подслово словакоторое само является формулой.

Лемма 1. Если и– формулы и– началотоДоказательство проведём индукцией по длине формулы т.е. по количеству символов, входящих вЕсли длина равна 1, то– атомарная формула, тогдатоже атомарная; очевидно, чтоЕслине атомарна, тоначинается либо слибо сПустьначинается с символаТогдагде– формула. Так как– началототакже начинается споэтомугде– формула. Очевидно,– началоЗначит, по предположению индукцииОтсюда следует, чтоНаконец, разберём случай, когданачинается с левой скобки.Тогда где– один из символоваи – формулы. Так как – началототакже начинается с левой скобки, а значит,гдеаи–формулы. Так как – началото либо– началолибо – начало В обоих случаях по предположению индукции получаемНо тогдаиОтсюда следует, что

Теорема 1. Всякая неатомарная формула единственным образом представима в одном из следующих видов:гдеи– формулы.Доказательство. Существование такого представления следует из определения формулы. Надо лишь доказать единственность. Понятно, что если представима в видето её нельзя представить в видеи надо лишь применить предположение индукции к формулеПустьпредставима в виденеоднозначно. ТогдаОдна из формулявляется началом другой. Значит, по лемме 1Но тогдаиЭто доказывает единственность.

Следствие. Пусть – формула ИВ. Тогда с каждым вхождением символаили символав эту формулу однозначно связывается вхождение вподформулы, начинающейся с этого символа.Доказательство. Действительно, если в есть символто при построении формулыранее была построена формуланачинающаяся с этого символа, причём– тоже формула. Формулакак раз и является подформулой, начинающейся с данного вхождениясимвола Единственность следует из леммы 1. Аналогично разбираются случаи вхождения всимвола (.

Теорема 2. Пусть – формула, аи– вхождения вкаких-либо подформул. Тогда либоине пересекаются, либо одно из них является подсловом другого.Доказательство. Пусть ипересекаются. Тогда либо первый символ извходит влибо наоборот . Пусть, например, первый символ извходит вЕслиатомарно, то– подслово словаеслиначинается сто по следствию из теоремы 1 весть подформуланачинающаяся с этого символа. По лемме 1совпадает сТогда– подслово словаАналогично разбирается случай, когданачинается с (

2. Правила вывода. Секвенции. Доказательства.

Секвенциями мы будем называть записи (последовательности значков) одного из следующих видов:

1. (2) (3)(4)

Здесь – формулы ИВ, знакчитается “выводится”. Секвенция (1) расшифровывается так: из формулвыводится формулаСеквенция (2) означает, что совокупность формулпротиворечива. Секвенция (3) означает, что формулавыводима.

Доказательства осуществляются на основе правил вывода, список которых мы приводим.

Правила вывода (здесь – какие-либо последовательности формул, возможно, пустые):

1.		7.
2.		8.
3.		9.
4.		10.
5.		11.
6.		12.

Аксиомами ИВ называются секвенции вида где– формула (не обязательно атомарная).

Доказательством называется последовательность секвенций

где каждая – либо аксиома, либо получается из секвенцийс помощью правил вывода.

Пример. Докажем, что Имеем:

Здесь – аксиома;получена изпо правилу 12;– аксиома;получается изпо 12;

– изпо 11 (считаем– изис помощью правила 1.

Лемма 2. Если секвенция доказуема (доказуема = выводима = существует для нее доказательство), то секвенциятакже доказуема.

Доказательство. Из по прав.7 получаем:Из аксиомыпо правилам 11, 12 (применённым, возможно, несколько раз) получаем:Затем изипо правилу 8 получаем:

Допустимые правила вывода.

(а)
(б)
(в)		(з)
(г)		(и)
(д)		(к)
(е)		(л)
(ж)		(м)

Докажем некоторые из этих правил:

(а) Доказательство этого правила получается применением правил 11 и 12.

(в)

Здесь (1) и (2) даны, (3) получается из (2) по правилу 7, а (4) – из (1) и (3) по правилу 8.

Заметим, что из (в) следует

(надо лишь в секвенции дописать слева формулы из

(г) Докажем это правило в упрощённом виде: когда

(1)		(аксиома);
(2)		(из (1) по 2);
(3)		(из (1) по 3);
(4)		(из (3) по 12);
(5)		(дано);
(6)		(из (5) по 11, 12);
(7)		(из (4) и (6) по (в));
(8)		(из (2) и (7) по (в)).

(д)

(1)		(дано);
(2)		(из (1) по 2);
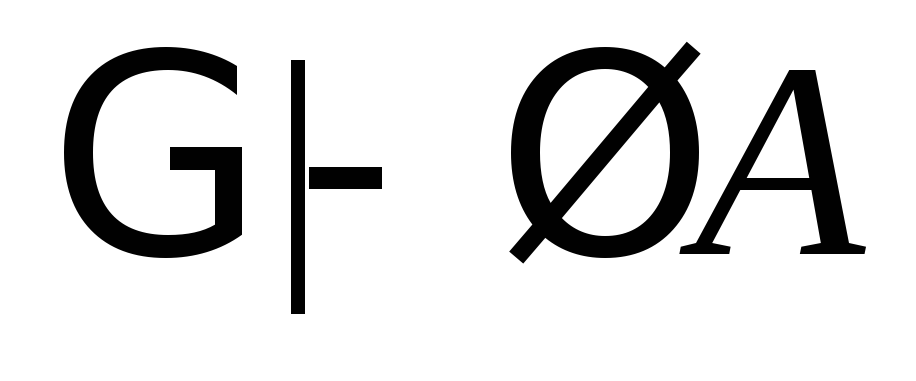
(3)		(из (1) по 3);
(4)		(из (2) и (3) по 10).

(ж) Для доказательства этого правила докажем лемму.

Лемма 3.

Доказательство. С помощью аксиом ипо правилам 11, 12 нетрудно получить, чтоиОтсюда по правилу 10 получаем:

Вернёмся к доказательству правила (ж). Нам надо доказать, что если секвенция имеет доказательство, тотакже имеет доказательство (оба доказательства должны основываться на правилах 1 – 12). Заметим, что получить секвенциюможно только по правилу 10. Значит, ранее были доказаны секвенцииидля некоторой формулыПропуская предыдущие шаги доказательства, будем иметь:

(1)
(2)
(3)		(из (1) по 12);
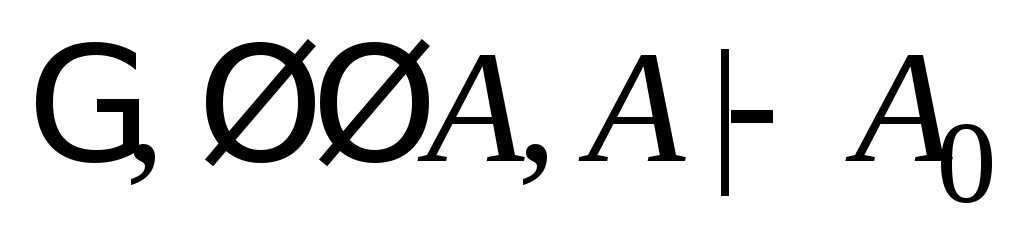
(4)		(из (3) по 11);
(5)		(из (4) по 7);
(6)		(по лемме 3);
(7)		(из (6) по 9);
(8)		(из (5) и (7) по 8);
(9) – (13)	шаги, аналогичные шагам (3) – (7), где вместо (1) взято (2);
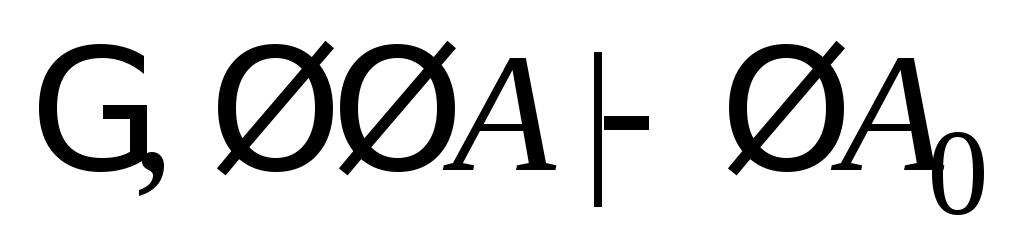
(14)		(аналогично (8));
(15)		(из (8) и (14) по10);
(16)		(из (15) по 9).

(б) Докажем один частный случай правила (б), а именно,

(1)		(дано);
(2)		(из (1) по (ж));
(3)		(из (2) по 11, 12);
(4)		(аксиома);
(5)		(из (4) по 12);
(6)		(из (3) и (5) по 10).

Важная секвенция (1). Для любой формулы доказуема секвенция

(1)		(аксиома);
(2)		(из (1) по 5);
(3)		(аксиома);
(4)		(из (2) по 12);
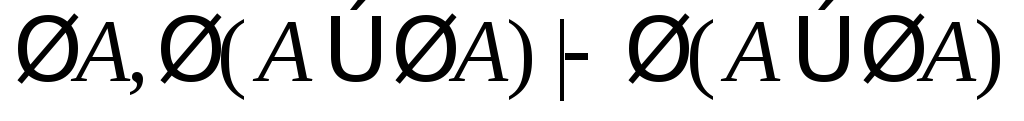
(5)		(из (3) по 11,12);
(6)		(из (4),(5) по 10);
(7)		(из (6) по 9, 11);
(8)		(из (7) по 4);
(9)		(из (3) и (8) по 10);
(10)		(из (9) по 9).

Важная секвенция (2). Для любой формулы доказуема секвенция

Доказательство.

(1)		(аксиома);
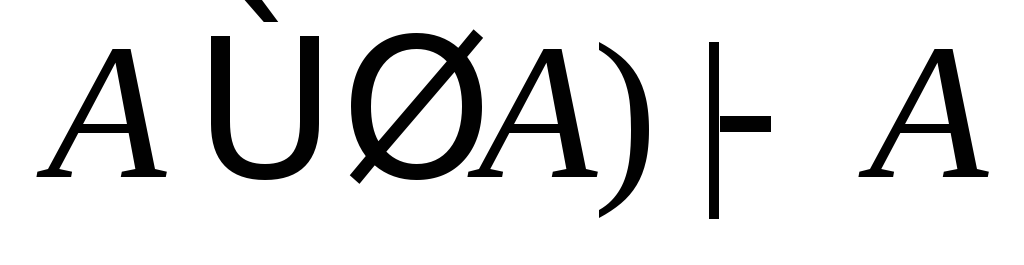
(2)		(из (1) по 2);
(3)		(из (1) по 3);
(4)		(из (2) и (3) по 10).

3. Эквивалентные формулы. Приведение формулы к нормальному виду.

Две формулы иназываютсяэквивалентными (обозначается: если доказуемы секвенциииСимволне принадлежит языку исчисления высказываний. Он принадлежитметаязыку, т.е. языку, на котором мы описываем исчисление высказываний.

Утверждение 1. Отношение является отношением эквивалентности.

Доказательство. Рефлексивность и симметричность отношения очевидны. Докажем его транзитивность. ПустьиТогдаТак какито по правилуАналогично получаемТаким образом,

Лемма 1 (о замене). Если ито

Доказательство. Докажем утверждение о конъюнкции:

(1)		(дано);
(2)		(дано);
(3)		(дано);
(4)		(дано);
(5)		(аксиома);
(6)		(из (5) по 3)
(7)		(из (5) по 3);
(8)		(из (6) и (1) по );
(9)		(из (7) и (3) по );
(10)		(из (8) и (9) по 1).

Секвенция доказывается аналогичным образом.

Теорема о замене: Если то любое вхождение формулыв более сложную формулуможет быть заменено на формулупричём новая формула будет эквивалентна формулеДоказательство осуществляется индукцией по длине формулы

Примеры доказательства эквивалентности формул.

1. Докажем, что

   (1)		(аксиома);
   (2)		(из (1) по 2);
   (3)		(из (1) по 3);
   (4)		(из (3) и (2) по 1).

2. Докажем, что

(1)		(аксиома);
(2)		(из (1) по 4).

В обратную сторону:

(1)		(аксиома);
(2)		(из (1) по 11, 12);
(3)		(то же самое);
(4)		(аксиома);
(5)		(из (2), (3), (4) по 6).

3. Докажем, что

(1)				(аксиома);
(2)				(аксиома);
(3)				(из (1) по 12);
(4)				(из (2) по 11, 12);
(5)				(из (3) и (4) по 10);
(6)				(из (5) по (е));
(7)				(аксиома);
(8)				(из (7) по 11, 12);
	(9)				(из (6) по 11, 12);
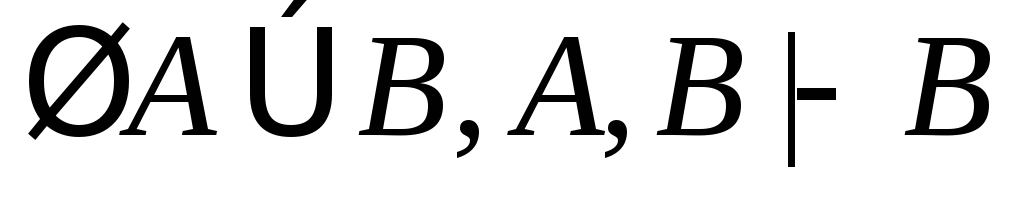
	(10)				(из (7) по 11, 12);
	(11)				(аксиома);
	(12)				(из (9),(10),(11) по 6);
	(13)				(из (12) по 7).

В обратную сторону:

(1)		(аксиома);
(2)		(аксиома);
(3)		(из (1) по 11, 12);
(4)		(из (2) по 12);
(5)		(из (3) и (4) по 8);
(6)		(из (5) по 5);
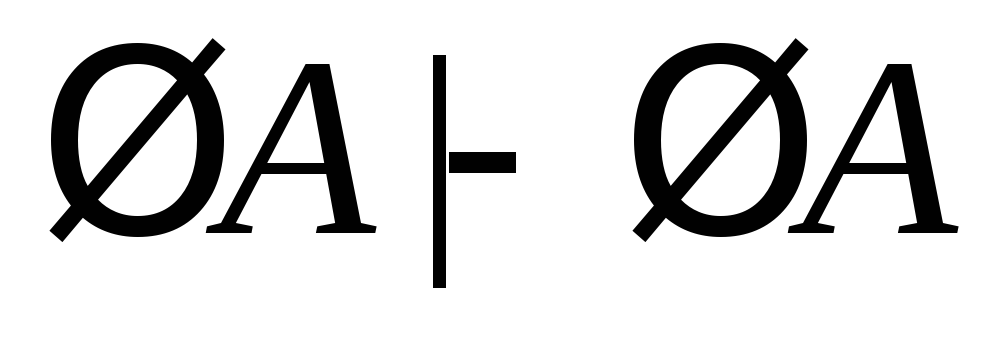
(7)		(аксиома);
(8)		(из (7) по 11, 12);
(9)		(из (8) по 4);
(10)		(лемма 4);
(11)		(из (10) по 12);
(12)		(из (6), (9), (11) по 6).

Еще есть такие эквивалентности:

Введём общее обозначение для формул игде– атомарная формула. А именно, положимПусть– атомарные формулы. Выражение видабудем называтьэлементарной дизъюнкцией, если слагаемые в этом выражении все разные. При этом, вообще говоря, формулы не обязательно различные. В частности, элементарными дизъюнкциями являются выражения

Теорема. Для всякой формулы рассматриваемой как выражение от атомарных формулсуществует формулатакая, чтои

где каждая скобка является элементарной дизъюнкцией.

P_i - атомарные формулы.P_iв одной скобке могут повторяться---отличие от СКНФ – там не может быть одновременноp_iиp_i.

Доказательство.

Вначале избавимся в формуле от знака импликациииспользуя эквивалентность

Далее, пользуясь законами де-Моргана а также законом двойного отрицаниямы сможем добиться того, чтобы знаки отрицаниястояли только при атомарных формулах.

(Кол-во перед атомарной формулой равно 0 или 1 (можно снять:). Будем считать, что внешняя операция -. Если внешняя -, то проносим внутрь, если (AB) неатомарны, то проносим дальше и т.д. ).

Можно их как угодно переставлять, пользуясь коммутативностью и тем, что преобразуем формулу далее.

И тогда конъюнкция будет равна произведению элементарных дизъюнкций.

\\\\\\\\\\\\\\Затем, используя дистрибутивность мы сможем сделать так, чтобы внешним действием была конъюнкция, т.е. получить выражение видаНаконец, благодаря эквивалентностяммы можем привести подобные члены, после чего каждая скобка вдействительно будет элементарной дизъюнкцией.— так в книжечке заканчивается\\\\\\\\\\\\\\\\\\\\\\\\\

4. Непротиворечивость классического ИВ.

Исчисление называется противоречивым, если существует формулатакая, что в этом исчислении доказуемы обе формулыиЕсли такой формулы нет, то исчисление называетсянепротиворечивым. Здесь под доказуемостью формулы понимается доказуемость секвенции

Семантика и синтаксис

В формальной математической теории действия, производимые над рассматриваемыми объектами в рамках самой теории, составляют синтаксис теории. Вопросы, выходящие за рамки формальной теории (например, интерпретация рассматриваемых понятий, “придание смысла” некоторым из них и т.д.), составляют семантику этой теории. В частности, формулы, секвенции, правила вывода, формальные доказательства – это синтаксис ИВ. Далее мы рассмотрим ряд семантических понятий.

Интерпретации ИВ

Пусть – непустое множество,– множество всех его подмножеств. Пусть– множество всех формул ИВ,– множество всех атомарных формул. Рассмотрим произвольное отображениеПродолжим его до отображенияа затем определимдля секвенций. Продолжениес атомарных формул на произвольные построим индуктивно, а именно: еслииуже построены, то полагаем:Итак, каждой формулеисчисления высказываний ставится в соответствие подмножествомножестваСеквенциям ИВ будем ставить в соответствие некоторыеутверждения о подмножествах множества а именно:

1. 

2. 

3. 

4. 

В вышеприведённых определениях принято следующее соглашение: если (т.е.тоОтметим, что так как множествопредполагается непустым, толожно (при любой интерпретации).

Проверим, что аксиомам в данной интерпретации будут поставлены в соответствие истинные утверждения, а применение правил вывода истинность утверждений не нарушает. В самом деле, аксиомы имеют вид поэтомуа это утверждение истинно. Для правил вывода сделаем выборочную проверку. Докажем, что если числителю правила вывода поставлены в соответствие истинные утверждения (о подмножествах множествато знаменателю также будет поставлено в соответствие истинное утверждение. В качестве примера возьмём правила 1 и 6.

Правило 1:

Пусть Еслито мы имеем:иНо тогдаа это означает, чтоистинно.

Правило 6:

Пусть Положим(приввиду наших соглашенийПо условиюиОтсюда получим

Теорема. Исчисление высказываний непротиворечиво.

Доказательство.

Предположим, что для какой-либо формулы доказуемы секвенциии

Рассмотрим какую-либо интерпретацию исчисления высказываний в множестве

Так как для аксиом утверждениеистинно и применение правил вывода не нарушает истинность секвенций, то для всех выводимых (т.е. доказуемых) секвенцийутверждениетакже истинно.

Значит, Поэтому

Но следовательно,что неверно. Таким образом, ИВ непротиворечиво.

5. Теорема о полноте.

6. Теорема о функциональной полноте ИВ.

Рассмотрим теперь главную интерпретацию ИВ. Это будет отображение где– множество всех формул, а– множество всех секвенций. Для атомарных формулзначениявыберем произвольным образом. На остальные формулы отображениераспространим по обычным правилам:гдеОтображениеможно рассматривать как присвоение значений истинности (“истина” или “ложь”) пропозициональным переменным. После того, как такое присвоение произошло, можно говорить об истинности или ложности других формул. Истинность или ложность секвенций определяется следующим образом:

1. либо при некоторомлибо

2. 

3. 

4. 

Сформулируем теперь эти определения другими словами. Пусть – формула ИВ, зависящая от пропозициональных переменных (атомарных формул) а– набор из 0 и 1. Будем говорить, чтоформула истинна на наборе если при. . . ,Пусть дана секвенцияи– пропозициональные переменные, входящие в какие-либо из формулСеквенцияистинна на наборе из 0 и 1, если на этом наборе либо хотя бы одно изложно, либоистинно. Далее, секвенцияистинна на наборе если хотя бы одна из формулна этом наборе ложна. Секвенцияистинна на данном наборе, если на этом наборе истинно. Наконец, секвенциясчитаетсяложной на любом наборе.

Отметим, что главная интерпретация является частным случаем интерпретации, рассмотренной ранее. Действительно, пусть состоит из одного элемента. ТогдаСчитаем для ф-лыеслииеслиНепосредственно проверяется, что получится главная интерпретация.

Формула (соответственно, секвенция) называетсятождественно истинной, если она истинна на любом наборе значений истинности пропозициональных переменных. Нетрудно видеть, что тождественная истинность формулы равносильна тождественной истинности секвенции

Лемма 1. Секвенция истинна на наборев том итолько в том случае, если секвенция истинна на этом наборе.

Док-во. Пусть истинна на набореТогда выполняется хотя бы одно из условий: 1) хотя бы одна из формул множестваложна на этом наборе; 2) формулаложна на этом наборе; 3) формулаистинна на этом наборе. Разберём эти случаи отдельно. 1) Если какая-нибудь формула изложна, тоистинна, а значит,истинна. 2) Еслиложна, тоистинна, поэтомуистинна. 3) Еслиистинна, тоистинна, а значит,также истинна.

Следствие. Секвенция тождественно истинна только в том случае, если секвенциятождественно истинна.

Лемма 2. Секвенция доказуема только в том случае, если секвенциядоказуема.

Док-во. Если секвенция имеет доказательство, то по правилу 7 это доказательство можно продолжить и получитьНаоборот, если доказана секвенциято из неё по правилу 12 получимУчитывая легко доказываемый фактпо правилу 8 получим

Лемма 3. а) Если секвенция доказуема, то она тождественно истинна;

б) если формула доказуема, то она тождественно истинна.

Док-во. Нетрудно проверить, что аксиомы являются тождественно-истинными секвенциями. Также легко проверяется, что применение правил вывода эту тождественную истинность не нарушает. Значит, любая выводимая (доказуемая) секвенция тождественно истинна. Утверждение, касающееся формул, сводится к уже доказанному для секвенций.

Лемма 4. Если формулы иэквивалентны, то булевы функцииисовпадают.

Док-во. Можно считать, что формулы изависят от одних и тех же пропозициональных переменных(переменные, которые не входят в формулу, считаем входящими фиктивно). По условиюи– доказуемые секвенции. По лемме 3 они тождественно истинны. Если на каком-либо набореформулаистинна, то так как секвенцияистинна, тона этом наборе тоже истинна. Аналогично доказывается, что еслиистинна на наборетотакже истинна на этом наборе. Итак,иистинны на одних и тех же наборах, значит,

Для формулы обозначим черезмножество наборовна которых она истинна.

Замечание. Лемма 4 на самом деле является следствием более общего результата: если для некоторых формул исеквенциядоказуема, то

Теорема 2 (о функциональной полноте ИВ). Пусть в исчислении высказываний бесконечно много атомарных формул. Тогда для любой булевой функции существует формулаисчисления высказываний, зависящая от атомарных формултакая, что

Доказательство. Если тождественно равна 0, то в качестве формулыможно взятьЕсли жето, как известно из курса дискретной математики,представима в совершенной дизъюнктивной нормальной форме:

Следовательно, в качестве формулы исчисления высказываний подойдёт формула

Из леммы 3 мы видели, что доказуемыми могут быть только тождественно истинные формулы или секвенции. Оказывается (и это мы докажем в следующей теореме), что верно и обратное: тождественно истинная формула или секвенция имеет формальное доказательство в ИВ. Этот факт мы будем называть полнотой исчисления высказываний.

Теорема 3 (о полноте ИВ).

(а) Формула исчисления высказываний доказуема тогда и только тогда, когда она тождественно истинна.

(б) Секвенция ИВ доказуема тогда и только тогда, когда она тождественно истинна.

Доказательство. Ввиду леммы 2 и следствия из леммы 1 доказуемости (соответственно, тождественные истинности) следующих секвенций эквивалентны: . . . Таким образом можно “перебросить” все формулы, стоящие слева от значкав правую часть и получить секвенцию видадля которой доказуемость (соответственно, тождественная истинность) равносильна доказуемости (соответственно, тождественной истинности) формулы(по определению). Следовательно, нам надо доказать только утверждение (а).

Ввиду леммы 3 нам следует доказать лишь достаточность: если формула тождественно истинна, то она доказуема. Пусть– тождественно истинная формула. По теореме 2 предыдущего раздела существует формулатакая, что

Положим . . . ,Так както по лемме 4тождественно истинна. Но это означает, что формулытождественно истинны. Рассмотрим какую-нибудь одну из них, например,Если всеразличны, тоне будет тождественно истинной, так как обращается в 0 на таком наборе, гдеЗначит, вкакая-либо пропозициональная переменная (скажем,встречается вместе со своим отрицанием. Следовательно,можно преобразовать:Секвенция доказуема по лемме 4 § 1.1. По правилу вывода 4 получим, что секвенция доказуема. Значит, формуладоказуема. Аналогично получим, что формулыдоказуемы. По правилу 1 получим, что формуладоказуема. Следовательно, формулаа значит, и формуладоказуема.

7. Разрешимость классического исчисления высказываний.

Под разрешимостью мы понимаем существование алгоритма, который по данной формуле (или секвенцииопределяет, доказуема эта формула (или секвенция) или нет. Такой алгоритм действительно существует.

Теорема 4. Исчисление высказываний разрешимо.

Доказательство. По теореме 3 (о полноте ИВ: (а) Формула исчисления высказываний доказуема тогда и только тогда, когда она тождественно истинна. (б) Секвенция ИВ доказуема тогда и только тогда, когда она тождественно истинна.) проверка доказуемости формулы или секвенции сводится к проверке её тождественной истинности. Алгоритм такой проверки очевиден: надо придавать пропозициональным переменным входящим в рассматриваемые формулы, всевозможные значения(из множестваи определять по таблицам истинности значение формулы(соответственно, секвенцииЕсли на любом наборе будем иметь(соответственно,то(соответственно,тождественно истинна, а значит, доказуема, в противном случае(илинедоказуема.

Замечание. Пусть формула тождественно истинна, в чём мы убедились, применив алгоритм, изложенный в теореме 4. Тогдаимеет доказательство. На самом делеможно построить алгоритм, выписывающий это доказательство (т.е. доказательство секвенции Алгоритм достаточно громоздкий, так как включает в себя (в качестве “подпрограмм”) доказательства утвержденийи многих других, ведь мы приводим формулук видудоказываем формулузатем продолжаем доказательство, пока не будет доказана формула

8. Исчисление высказываний гильбертовского типа.

Рассмотрим ещё одну формализацию исчисления высказываний. Она была предложена Д.Гильбертом и включает одиннадцать схем аксиом и одно правило вывода (напомним, что в генценовском ИВ одна схема аксиом и двенадцать правил вывода). В гильбертовском ИВ определение формулы то же, что в генценовском. Мы пока не вводим здесь секвенции и говорим о выводимости (доказуемости) самой формулы. По определению выводимыми являются аксиомы и те формулы, которые получаются из аксиом и уже доказанных формул с помощью единственного правила вывода.

Схемы аксиом гильбертовского ИВ

(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)

Исчисление, использующее аксиомы (1) – (11), называется классическим исчислением высказываний (ИВ), аксиомы (1) – (10) определяют интуиционистское исчисление высказываний (ИИВ).