5. Определение максимального значения выходной величины исследуемого процесса.

Для определения максимального значения выходной величины исследуемого процесса используется метод крутого восхождения.

1. Д 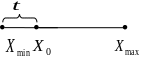ля перехода от естественных к кодированным координатам необходимо ввести значения 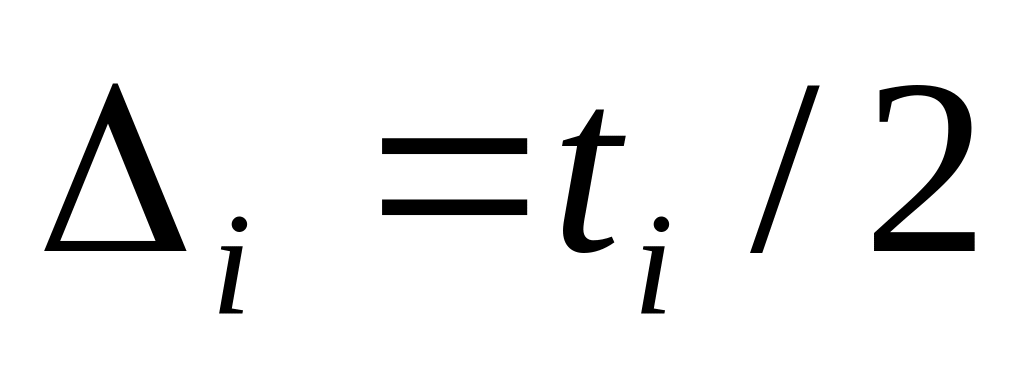для всех факторов, где определяется как

2. В задании число исследуемых параметров равно 6, значит, число экспериментов в матрице плана полного факторного эксперимента будет равно 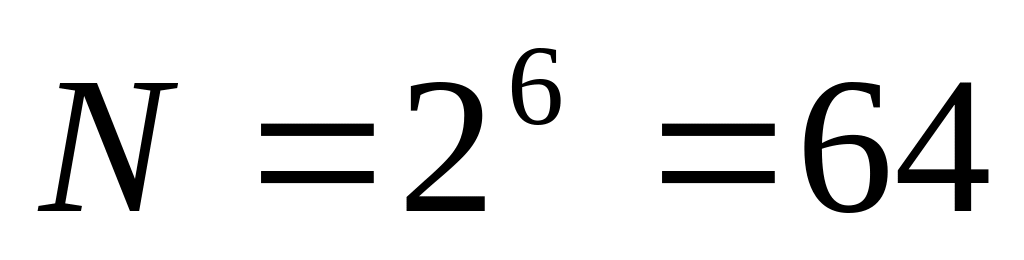, а в соответствии с математической моделью применяемой в методе крутого восхождения:

.

Поэтому данный план будет избыточным и число экспериментов целесообразно сократить, воспользовавшись матрицей плана дробного факторного эксперимента.

3. Для составления матрицы плана дробного факторного эксперимента необходимо определить генерирующие соотношения, поэтому в базовой точке проводится полный факторный эксперимент по плану:

№
1	-1	-1	-1	-1	-1	-1
2	1	-1	-1	-1	-1	-1
3	-1	1	-1	-1	-1	-1
4	1	1	-1	-1	-1	-1
5	-1	-1	1	-1	-1	-1
6	1	-1	1	-1	-1	-1
7	-1	1	1	-1	-1	-1
8	1	1	1	-1	-1	-1
9	-1	-1	-1	1	-1	-1
10	1	-1	-1	1	-1	-1
11	-1	1	-1	1	-1	-1
12	1	1	-1	1	-1	-1
13	-1	-1	1	1	-1	-1
14	1	-1	1	1	-1	-1
15	-1	1	1	1	-1	-1
16	1	1	1	1	-1	-1
17	-1	-1	-1	-1	1	-1
18	1	-1	-1	-1	1	-1
19	-1	1	-1	-1	1	-1
20	1	1	-1	-1	1	-1
21	-1	-1	1	-1	1	-1
22	1	-1	1	-1	1	-1
23	-1	1	1	-1	1	-1
24	1	1	1	-1	1	-1
25	-1	-1	-1	1	1	-1
26	1	-1	-1	1	1	-1
27	-1	1	-1	1	1	-1
28	1	1	-1	1	1	-1
29	-1	-1	1	1	1	-1
30	1	-1	1	1	1	-1
31	-1	1	1	1	1	-1
32	1	1	1	1	1	-1
33	-1	-1	-1	-1	-1	1
34	1	-1	-1	-1	-1	1
35	-1	1	-1	-1	-1	1
36	1	1	-1	-1	-1	1
37	-1	-1	1	-1	-1	1
38	1	-1	1	-1	-1	1
39	-1	1	1	-1	-1	1
40	1	1	1	-1	-1	1
41	-1	-1	-1	1	-1	1
42	1	-1	-1	1	-1	1
43	-1	1	-1	1	-1	1
44	1	1	-1	1	-1	1
45	-1	-1	1	1	-1	1
46	1	-1	1	1	-1	1
47	-1	1	1	1	-1	1
48	1	1	1	1	-1	1
49	-1	-1	-1	-1	1	1
50	1	-1	-1	-1	1	1
51	-1	1	-1	-1	1	1
52	1	1	-1	-1	1	1
53	-1	-1	1	-1	1	1
54	1	-1	1	-1	1	1
55	-1	1	1	-1	1	1
56	1	1	1	-1	1	1
57	-1	-1	-1	1	1	1
58	1	-1	-1	1	1	1
59	-1	1	-1	1	1	1
60	1	1	-1	1	1	1
61	-1	-1	1	1	1	1
62	1	-1	1	1	1	1
63	-1	1	1	1	1	1
64	1	1	1	1	1	1

Для данного плана полного факторного эксперимента используется регрессионная зависимость:

1. Необходимо провести обработку результатов экспериментов и проверить данную регрессионную модель на адекватность:

   1. Обработка экспериментальных данных

      1. Определение среднего значения в каждой точке плана

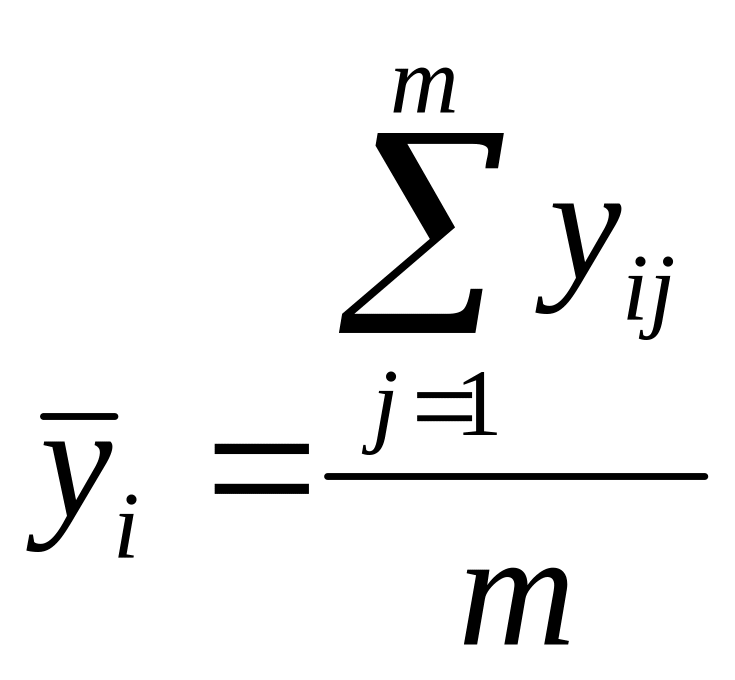
2. Определение дисперсии полученных экспериментальных данных , относительно усредненного значения:

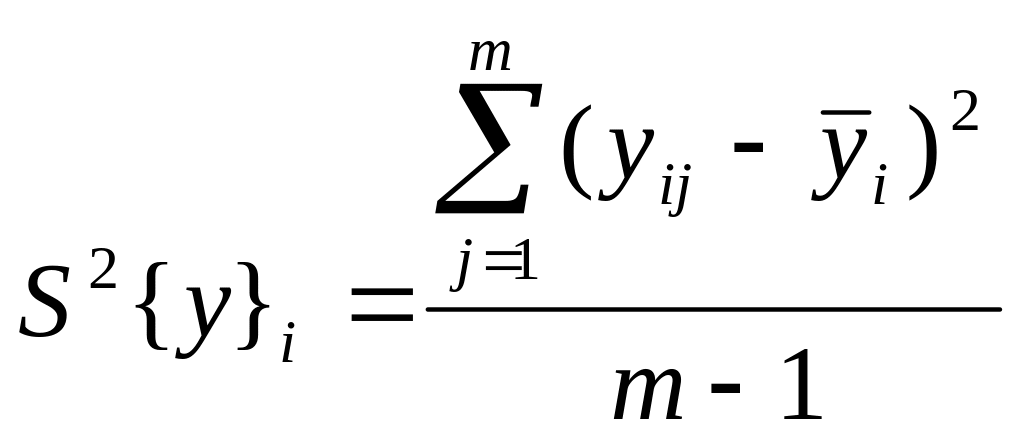
3. Определение достоверности полученных данных. Воспользуемся критерием Кохрена, согласно этому критерию определяется однородность дисперсий экспериментальных данных, если дисперсия результатов эксперимента неоднородна, значит, в эксперименте допущены грубые промахи, либо не учтен какой-то влияющий фактор.

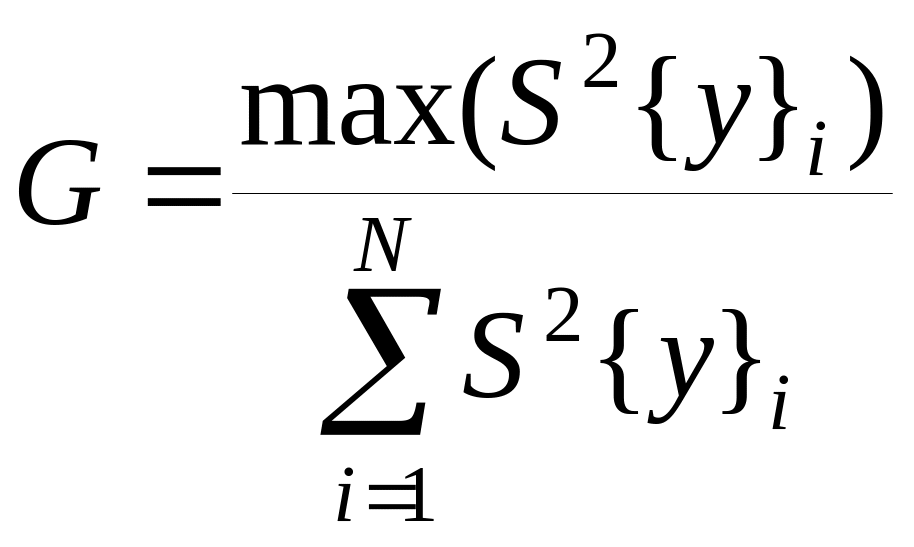
При , где

– расчетное значение критерия Кохрена

– теоретическое значение критерия Кохрена,

если данное условие выполняется, значит, дисперсия экспериментальных данных однородна.

4. Определение дисперсии воспроизводимости всего плана эксперимента:

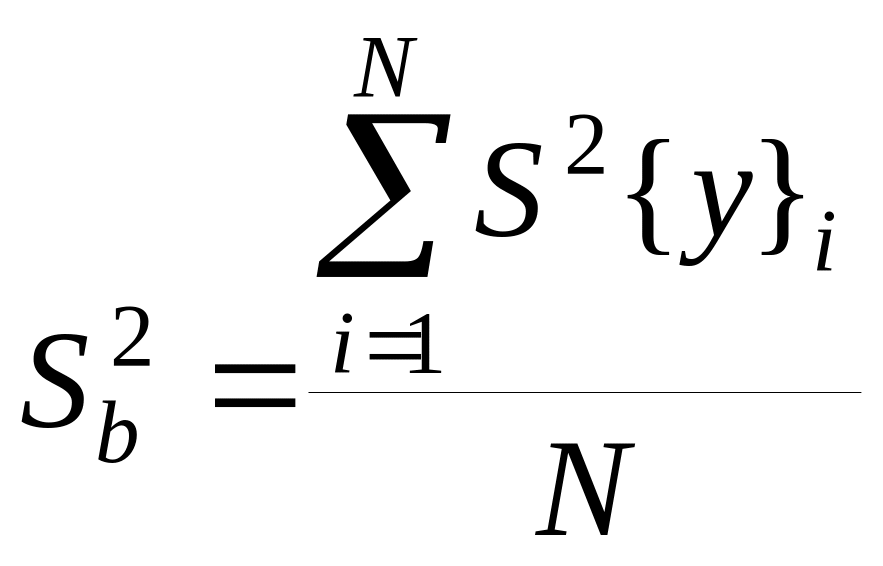
5. Определение дисперсии ошибки в определении коэффициентов, рассчитываемых по формуле:

6. Определение оценок коэффициентов:

, , ,

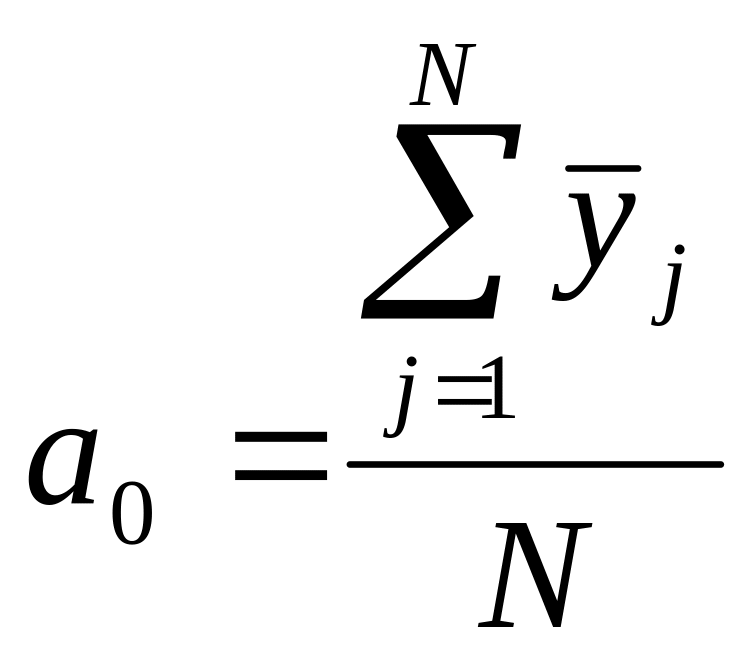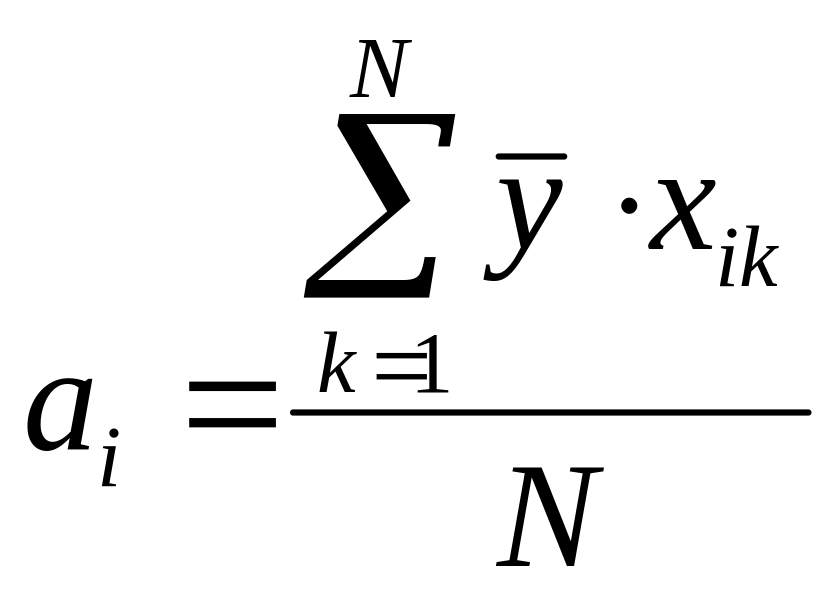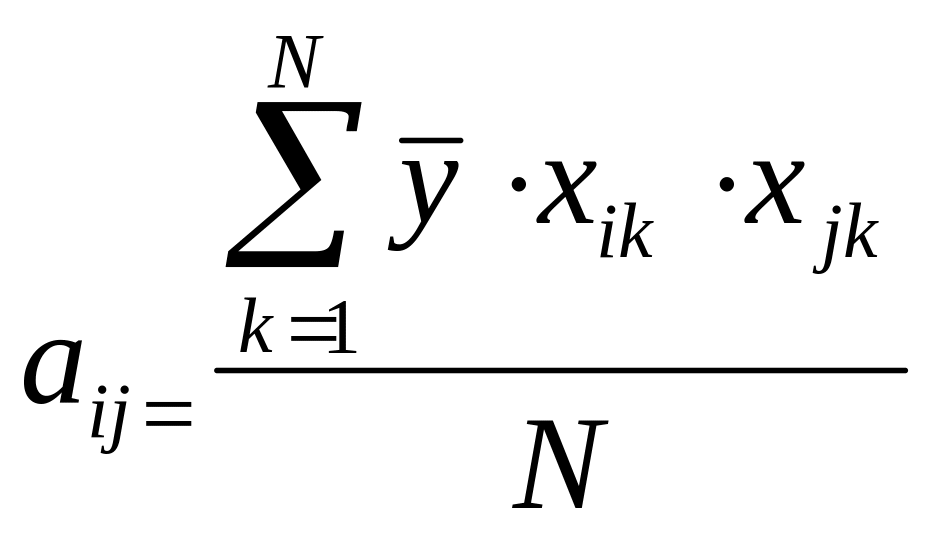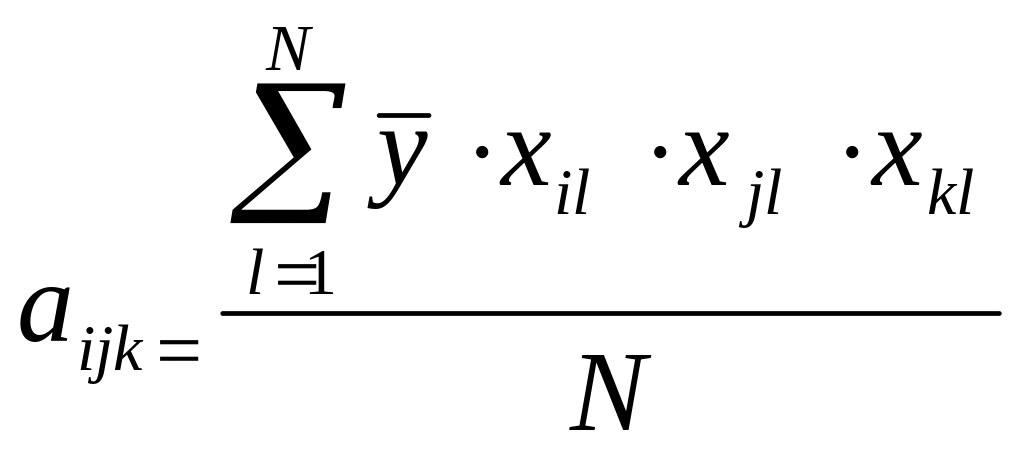
7. Определение статистической значимости оценок коэффициентов регрессионной зависимости по критерию Стьюдента:

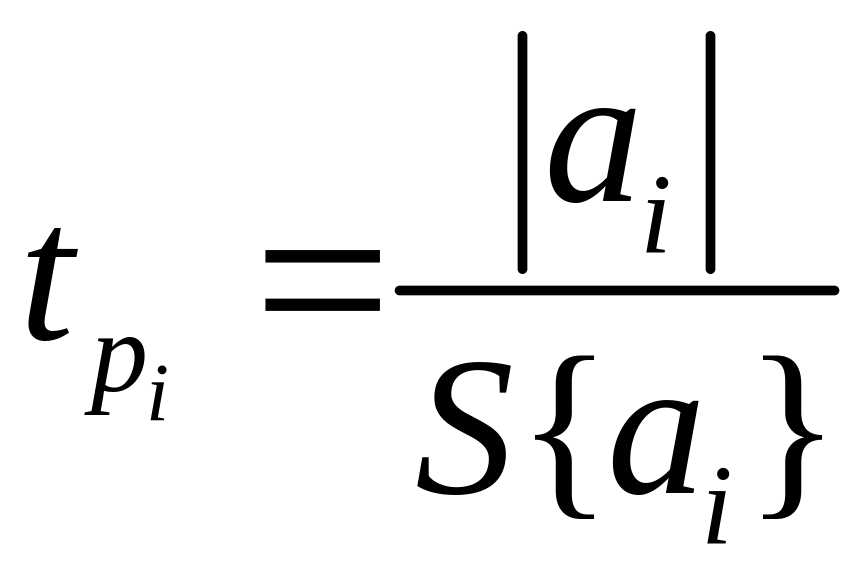
если – значит этот коэффициент незначимый и исключается из математической модели.

2. Проверка регрессионной зависимости на адекватность:

   1. Определение теоретических значений 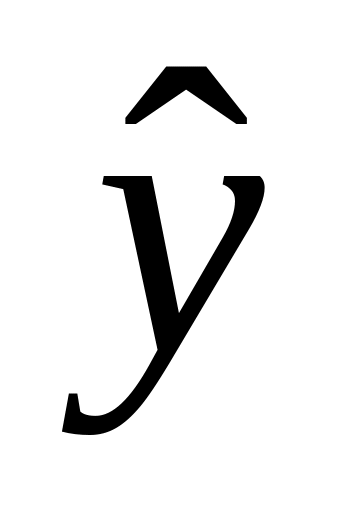в каждой точке плана по регрессионной зависимости:

2. Определение дисперсии адекватности математической модели:

,

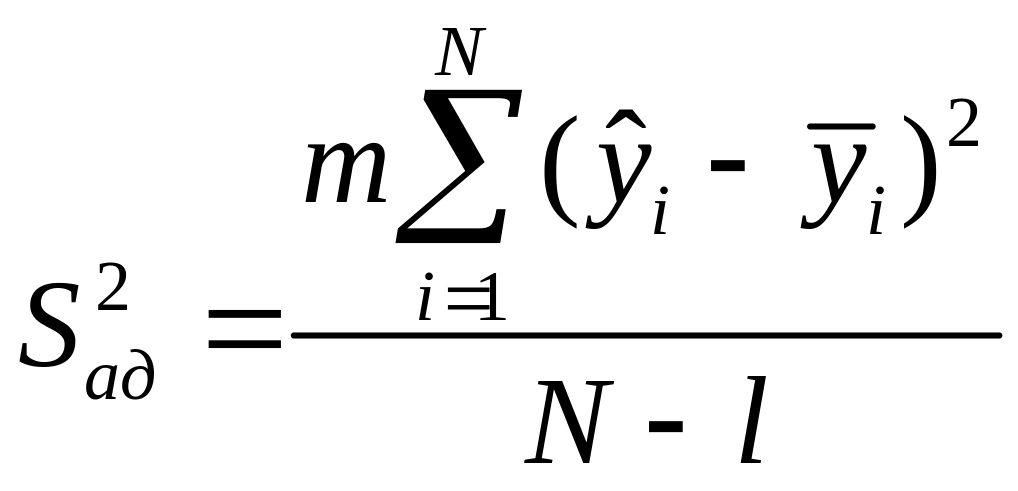где l – количество значимых коэффициентов. Дисперсия адекватности показывает, насколько велик разброс значений между теоретической моделью и результатами эксперимента.

3. Определение адекватности математической модели по критерию Фишера:

,

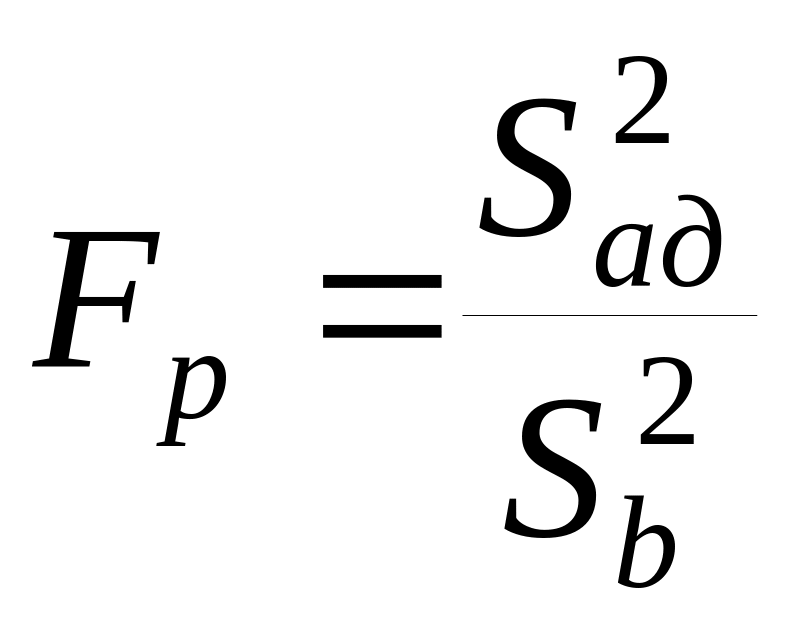если , то математическая модель адекватна, если математическая модель неадекватна необходимо уменьшить .

2. Для составления плана дробного факторного эксперимента типа 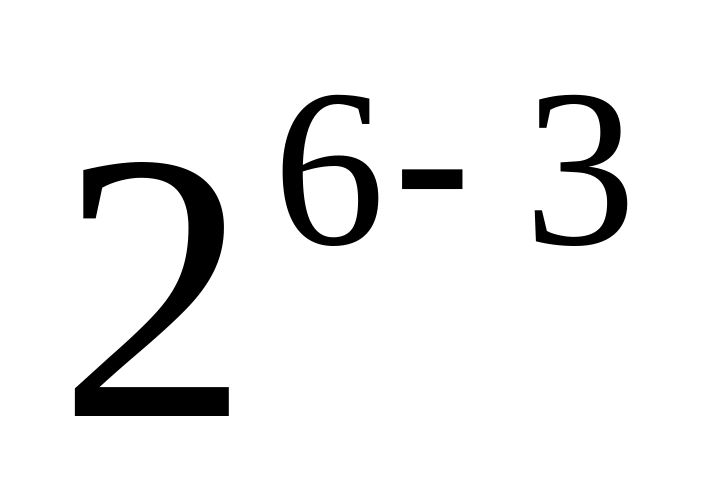необходимо взять три основных фактора и три фактора полученные при помощи генерирующих соотношений. Основными факторами выбираются те факторы, у которых оценки коэффициентов наиболее статистически значимы, а генерирующие соотношения выбираются на основе парных и тройных взаимодействий основных факторов, причем выбираются те сочетания факторов, у которых оценки коэффициентов наименее статистически значимы.

1. В соответствии с методом крутого восхождения по полученному плану дробного факторного эксперимента определяются оценки коэффициентов и адекватность регрессионной зависимости в соответствии с п. 3.1.

2. Неадекватности регрессионной зависимости или статистическая не значимость коэффициентов 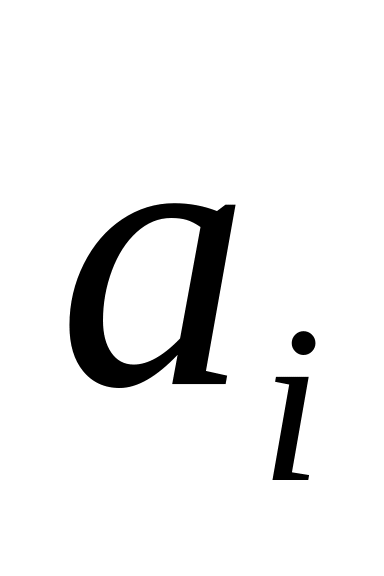являются признаком достижения глобального экстремума.

3. Если глобальный экстремум не достигнут осуществляется переход к следующей базовой точке:

   1. Вводится шаг варьировани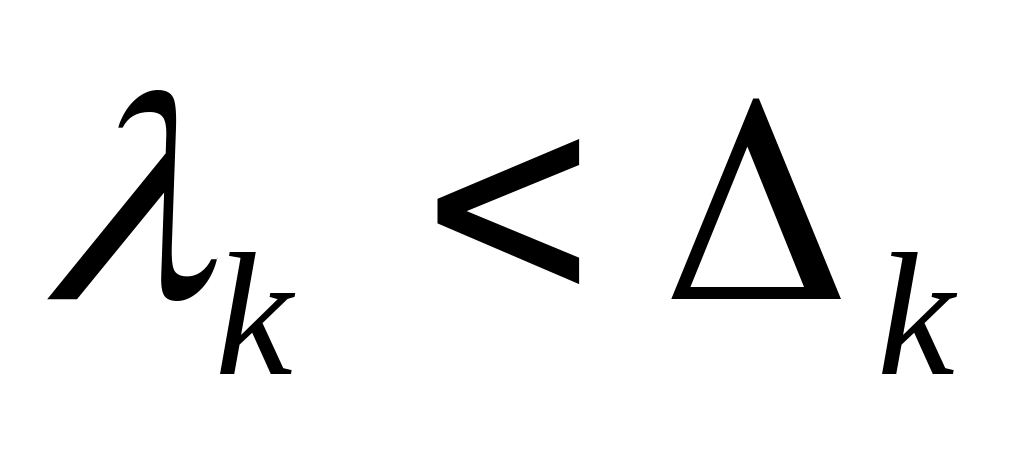я для 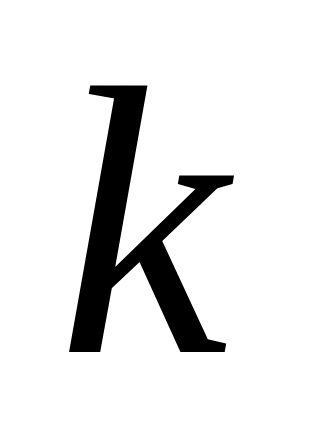-того фактора, причем

   2. Рассчитывается нормированный шаг

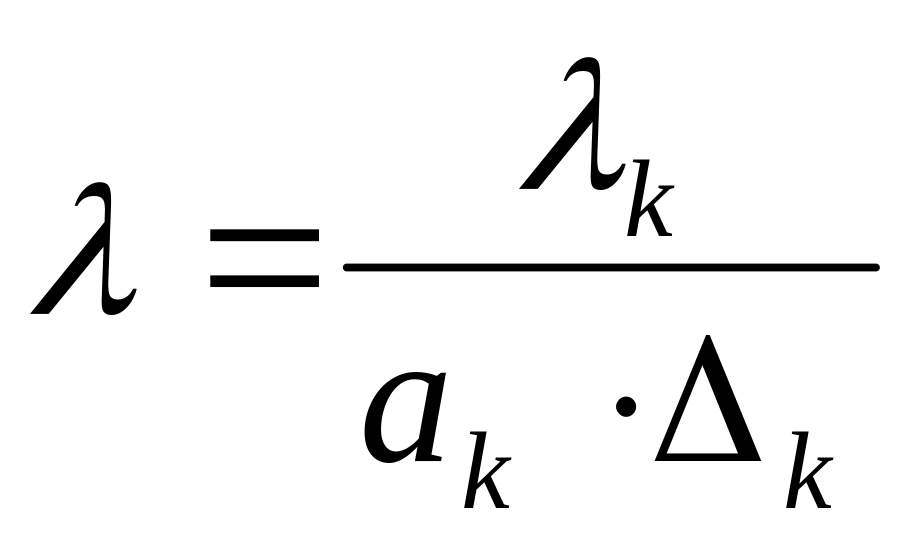
   3. Рассчитываются шаги в естественных координатах для остальных факторов

4. Определяются координаты следующей базовой точки

5. Рассчитывается абсолютная погрешность функции отклика в смежных базовых точках

6. Если выполняется услови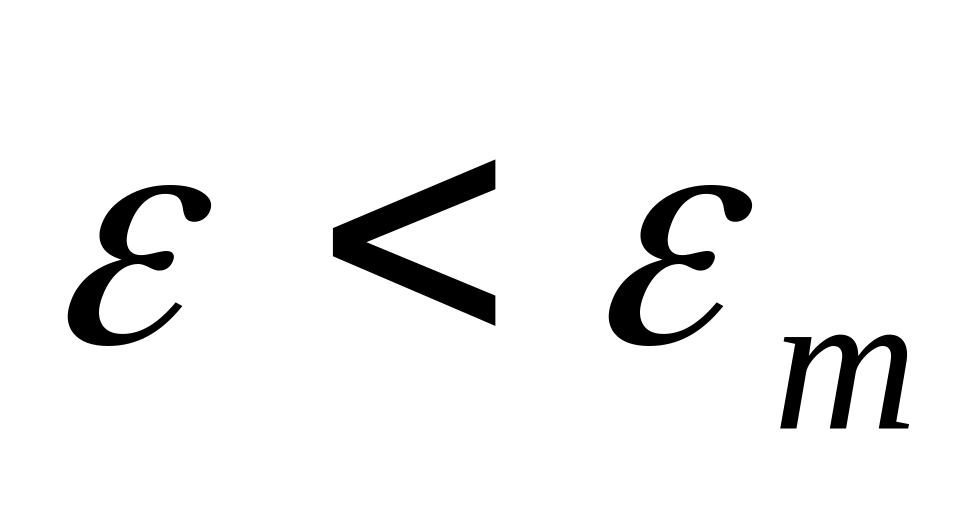е , где 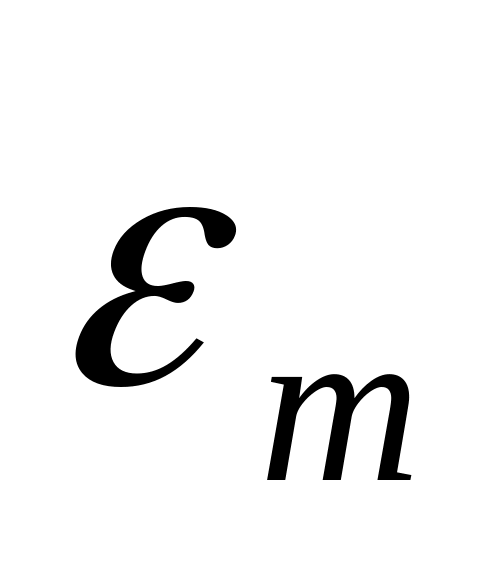– допустимая погрешность, то расчет заканчивается

7. Если после перехода к новой базовой точке выполняется условие 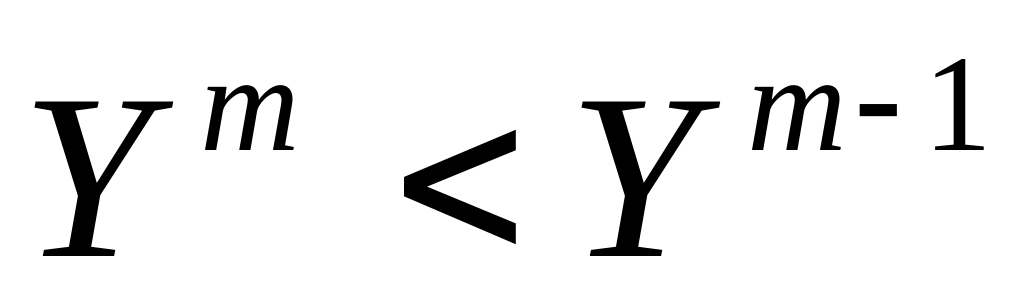необходимо уменьшить

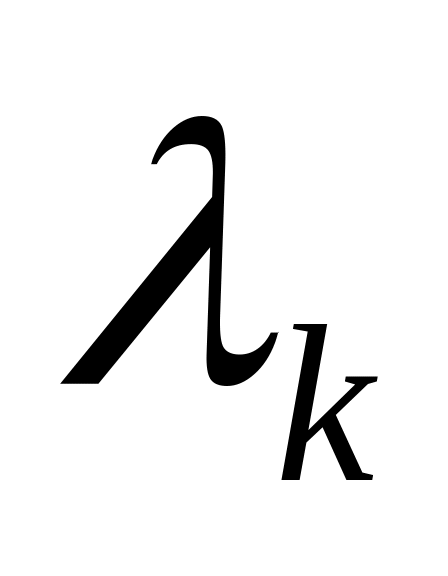
8. Если не выполняется условие в п. 6.6 то проводится дробный факторный эксперимент в новой базовой точке.

1. Рассчитывается максимальное значение в последней базовой точке