Минимизация издержек исследований.
Минимизация издержек исследований проводится за счет выбора стратегии проведения экспериментов на основе заданного критерия оптимальности.
Рассмотрим следующий пример: определить стратегию проведения эксперимента для 8 опытов при следующих условиях:
Имеется установки двух типов в количестве I типа 2 шт., II типа 2 шт. и неограниченное количество операторов 1 и 2 разрядов,
Оператор |
Себестоимость работы, руб/ч |
|
Установка |
Себестоимость работы, руб/ч |
Время работы, ч |
1 разряд |
219 |
1 тип |
289 |
14 |
|
2 разряд |
178 |
2 тип |
342 |
20 |
критерий
оптимальности издержек:
где
,
,
коэффициенты весомости: 0,76 0,24
Наиболее оптимальную стратегию проведения эксперимента определим переборов всех возможных вариантов. Для этого:
составим все возможные стратегии проведения эксперимента при помощи программы, приведенной в приложении 1.
Кол-во
опытов
I тип с оператором 1 разряд |
Кол-во
опытов
I тип с оператором 2 разряд |
Кол-во
опытов
II тип с оператором 1 разряд |
Кол-во
опытов
II тип с оператором 2 разряд |
Время проведения экспериментов T, ч |
Себестоимость экспериментов C, руб |
Критерий оптимальности |
4 |
4 |
0 |
0 |
56 |
54600 |
1,096 |
4 |
3 |
1 |
0 |
56 |
59282 |
1,161 |
3 |
4 |
1 |
0 |
56 |
58708 |
1,153 |
4 |
2 |
2 |
0 |
42 |
63964 |
1,142 |
3 |
3 |
2 |
0 |
42 |
63390 |
1,134 |
2 |
4 |
2 |
0 |
42 |
62816 |
1,126 |
4 |
1 |
3 |
0 |
42 |
68646 |
1,208 |
3 |
2 |
3 |
0 |
42 |
68072 |
1,200 |
2 |
3 |
3 |
0 |
42 |
67498 |
1,192 |
1 |
4 |
3 |
0 |
42 |
66924 |
1,184 |
4 |
0 |
4 |
0 |
40 |
73328 |
1,261 |
3 |
1 |
4 |
0 |
40 |
72754 |
1,253 |
2 |
2 |
4 |
0 |
40 |
72180 |
1,245 |
1 |
3 |
4 |
0 |
40 |
71606 |
1,237 |
0 |
4 |
4 |
0 |
40 |
71032 |
1,229 |
4 |
3 |
0 |
1 |
56 |
58462 |
1,150 |
3 |
4 |
0 |
1 |
56 |
57888 |
1,142 |
4 |
2 |
1 |
1 |
42 |
63144 |
1,131 |
3 |
3 |
1 |
1 |
42 |
62570 |
1,123 |
2 |
4 |
1 |
1 |
42 |
61996 |
1,115 |
4 |
1 |
2 |
1 |
42 |
67826 |
1,196 |
3 |
2 |
2 |
1 |
42 |
67252 |
1,188 |
2 |
3 |
2 |
1 |
42 |
66678 |
1,180 |
1 |
4 |
2 |
1 |
42 |
66104 |
1,172 |
4 |
0 |
3 |
1 |
40 |
72508 |
1,249 |
3 |
1 |
3 |
1 |
40 |
71934 |
1,241 |
2 |
2 |
3 |
1 |
40 |
71360 |
1,233 |
1 |
3 |
3 |
1 |
40 |
70786 |
1,225 |
0 |
4 |
3 |
1 |
40 |
70212 |
1,217 |
3 |
0 |
4 |
1 |
60 |
76616 |
1,426 |
2 |
1 |
4 |
1 |
60 |
76042 |
1,418 |
1 |
2 |
4 |
1 |
60 |
75468 |
1,410 |
0 |
3 |
4 |
1 |
60 |
74894 |
1,402 |
4 |
2 |
0 |
2 |
42 |
62324 |
1,120 |
3 |
3 |
0 |
2 |
42 |
61750 |
1,112 |
2 |
4 |
0 |
2 |
42 |
61176 |
1,104 |
4 |
1 |
1 |
2 |
42 |
67006 |
1,185 |
3 |
2 |
1 |
2 |
42 |
66432 |
1,177 |
2 |
3 |
1 |
2 |
42 |
65858 |
1,169 |
1 |
4 |
1 |
2 |
42 |
65284 |
1,161 |
4 |
0 |
2 |
2 |
40 |
71688 |
1,238 |
3 |
1 |
2 |
2 |
40 |
71114 |
1,230 |
2 |
2 |
2 |
2 |
40 |
70540 |
1,222 |
1 |
3 |
2 |
2 |
40 |
69966 |
1,214 |
0 |
4 |
2 |
2 |
40 |
69392 |
1,206 |
3 |
0 |
3 |
2 |
60 |
75796 |
1,415 |
2 |
1 |
3 |
2 |
60 |
75222 |
1,407 |
1 |
2 |
3 |
2 |
60 |
74648 |
1,399 |
0 |
3 |
3 |
2 |
60 |
74074 |
1,391 |
2 |
0 |
4 |
2 |
60 |
79904 |
1,472 |
1 |
1 |
4 |
2 |
60 |
79330 |
1,464 |
0 |
2 |
4 |
2 |
60 |
78756 |
1,456 |
4 |
1 |
0 |
3 |
42 |
66186 |
1,173 |
3 |
2 |
0 |
3 |
42 |
65612 |
1,165 |
2 |
3 |
0 |
3 |
42 |
65038 |
1,157 |
1 |
4 |
0 |
3 |
42 |
64464 |
1,149 |
4 |
0 |
1 |
3 |
40 |
70868 |
1,226 |
3 |
1 |
1 |
3 |
40 |
70294 |
1,218 |
2 |
2 |
1 |
3 |
40 |
69720 |
1,210 |
1 |
3 |
1 |
3 |
40 |
69146 |
1,202 |
0 |
4 |
1 |
3 |
40 |
68572 |
1,194 |
3 |
0 |
2 |
3 |
60 |
74976 |
1,404 |
2 |
1 |
2 |
3 |
60 |
74402 |
1,396 |
1 |
2 |
2 |
3 |
60 |
73828 |
1,388 |
0 |
3 |
2 |
3 |
60 |
73254 |
1,380 |
2 |
0 |
3 |
3 |
60 |
79084 |
1,461 |
1 |
1 |
3 |
3 |
60 |
78510 |
1,453 |
0 |
2 |
3 |
3 |
60 |
77936 |
1,445 |
1 |
0 |
4 |
3 |
80 |
83192 |
1,638 |
0 |
1 |
4 |
3 |
80 |
82618 |
1,630 |
4 |
0 |
0 |
4 |
40 |
70048 |
1,215 |
3 |
1 |
0 |
4 |
40 |
69474 |
1,207 |
2 |
2 |
0 |
4 |
40 |
68900 |
1,199 |
1 |
3 |
0 |
4 |
40 |
68326 |
1,191 |
0 |
4 |
0 |
4 |
40 |
67752 |
1,183 |
3 |
0 |
1 |
4 |
60 |
74156 |
1,392 |
2 |
1 |
1 |
4 |
60 |
73582 |
1,384 |
1 |
2 |
1 |
4 |
60 |
73008 |
1,376 |
0 |
3 |
1 |
4 |
60 |
72434 |
1,368 |
2 |
0 |
2 |
4 |
60 |
78264 |
1,449 |
1 |
1 |
2 |
4 |
60 |
77690 |
1,441 |
0 |
2 |
2 |
4 |
60 |
77116 |
1,433 |
1 |
0 |
3 |
4 |
80 |
82372 |
1,627 |
0 |
1 |
3 |
4 |
80 |
81798 |
1,619 |
0 |
0 |
4 |
4 |
80 |
86480 |
1,684 |
на
установке
на
установке
на
установке
на
установке
Исходя из того, что опыты можно проводить параллельно суммарное время проведения экспериментов можно определить по формуле:
,
где ОКРУГЛВВЕРХ() – функция, которая округляет число до ближайшего целого большего по модулю,
– время работы первой установки,
– время работы второй установки.
Суммарная себестоимость экспериментов рассчитывается по формуле:
,
где
– себестоимость работы 1 часа на установке
I –типа,
– себестоимость работы 1 часа установке
II – типа,
– себестоимость работы 1 часа оператора
1 разряда,
– себестоимость работы 1 часа оператора
2 разряда.
Находим минимальные значения времени и себестоимости проведения экспериментов и рассчитываем критерий оптимальности.
Определяем стратегию проведения экспериментов, для которой критерий оптимальности минимальный:
,
,
,
,
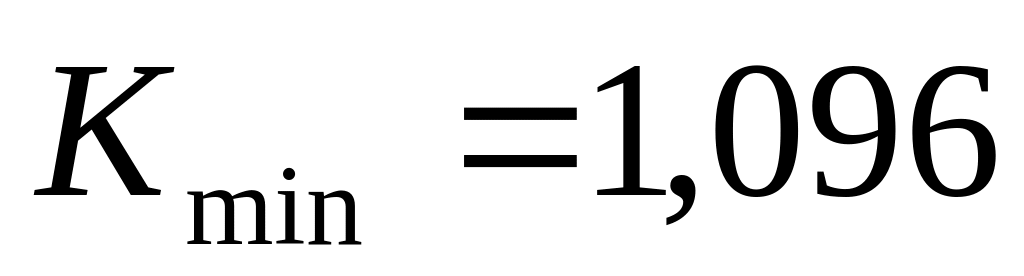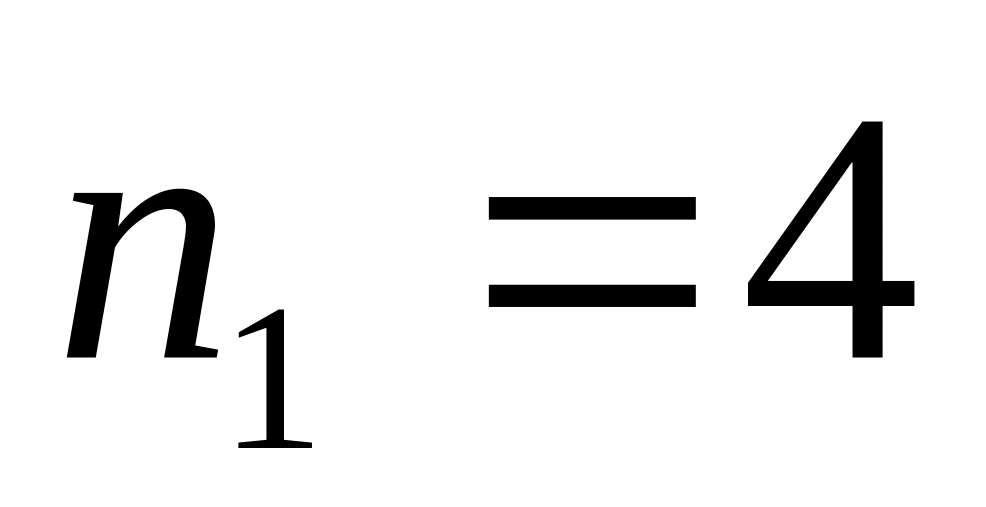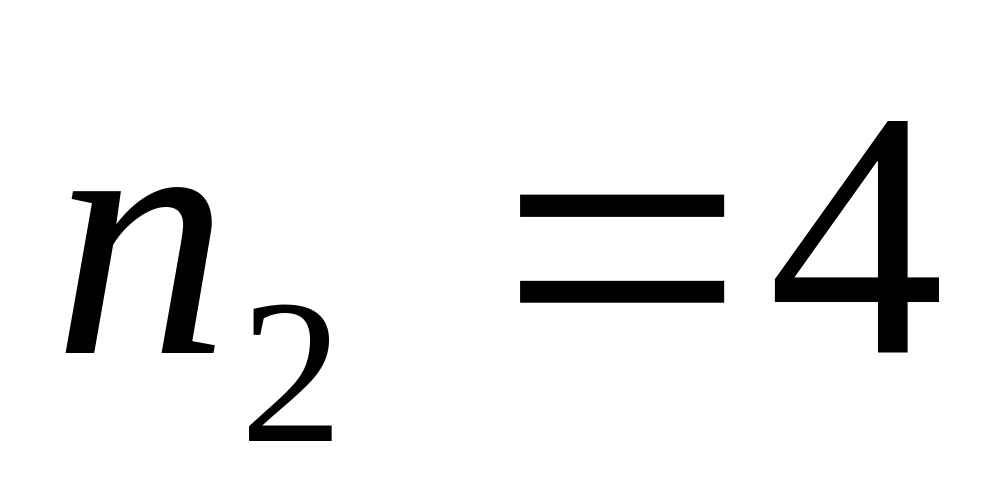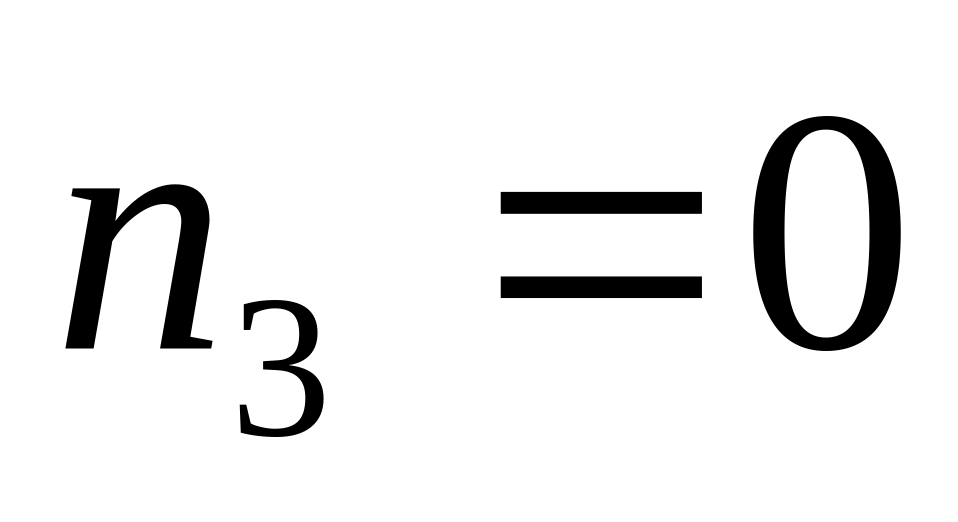