8.8. Свойства дифференциала функции
1.
Имеется
тесная связь между дифференциалом
функции и её производной. Для того чтобы
функция от одного переменного
имела в точке
дифференциал, необходимо
и достаточно,
чтобы она имела в этой точке (конечную)
производную
,
и было справедливо равенство:
.
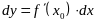Таким образом, правила нахождения дифференциалов непосредственно вытекают из соответствующих правил нахождения производных.
2.
,
где
– дифференциал константы равен нулю.
Доказательство.
.
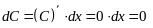3.
–
постоянный множитель можно выносить
за знак дифференциала.
Доказательство.
.
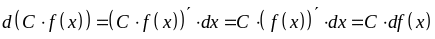4.
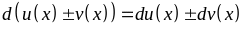– дифференциал от суммы или разности
двух функций равен сумме или разности
дифференциалов этих функций.
Доказательство.
.
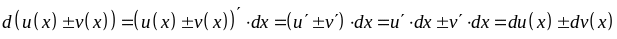5.
–
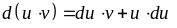дифференциал от произведения двух
функций равен сумме произведения
дифференциала от первой функции,
умноженному на вторую функцию и
произведения первой функции умноженному
на дифференциал от второй функции.
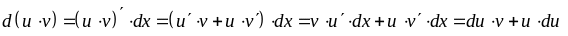
6.
– дифференциал от частного двух функций
равен дроби, в числителе которой стоит
разность произведений второй функции,
умноженной на дифференциала от первой
функции, и произведения первой функции
умноженному на дифференциал от второй
функции, а в знаменателе стоит квадрат
второй функции. Доказательство.
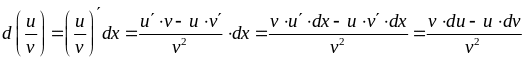
8.9. Дифференциал от сложной функции
Теорема 8.4. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Доказательство.
Рассмотрим
две дифференцируемые
функци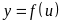и
и
,
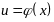которые образуют сложную функцию
.
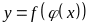По замечанию 8.6 к
теореме 8.3 о дифференцируемости сложной
функции можно записать её производную:
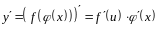или короче ,
(значком внизу обозначена переменная,
по которой вычисляется производная).
Умножая обе части
равенства производной сложной функции
на
и замечая, что
,
получаем формулу для вычисления
дифференциала
сложной функции
. (8.5)
8.10 Инвариантности формы первого дифференциала
Заметим,
что в формуле (8.5) произведение
.
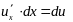Следовательно, дифференциал сложной функции
или
.
Последние
формулы обладают
замечательным свойством, именно:
формула дифференциала
не
изменяется, если вместо независимой
переменной
,
рассматривать
функцию от
переменной
.
Это свойство дифференциала получило
название инвариантности
формы
первого дифференциала. Теорема 8.4
доказана.
8.11. Применение дифференциала к приближенным вычислениям
Дифференциал функции может применяться для приближенных вычислений.
В
замечании
8.8 отмечалось, в общем случае, разность
между приращением и дифференциалом
функции является бесконечно малой
высшего порядка малости, чем приращение
аргумента:
.
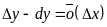Поэтому, при
достаточно малых значениях приращения
аргумента
,
можно считать, что
.
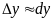Это означает,
что
,
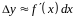т.е. при малых
изменениях аргумента (от начального
значения
),
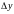– величину
изменения функции
,
можно приближенно
считать пропорциональной величине
изменения аргумента с коэффициентом
пропорциональности, равным значению
производной
.
Таким образом; в точке
кривую графика
функции
можно приближенно заменить касательной
к ней.
Формула
эквивалентна формуле
.
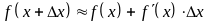