8.6. Дифференциал функции

Пусть функция 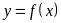– дифференцируема в точке , тогда её приращение этой функции в точке 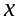, соответствующее приращению аргумента 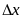, может быть представлено в виде

, (8.1)

где – некоторое число, не зависящее о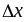т , а – функция аргумента , которая является бесконечно малой при .

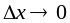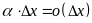Таким образом, приращение функции представляет собой сумму двух бесконечно малых слагаемых и . Было показано, что второе слагаемое является бесконечно малой функцией более высокого порядка, чем т.е. (см. 8.1). Поэтому первое слагаемое является главной линейной частью приращения 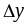функции . В замечании 8.1. получена другая формула (8.1.1) для приращения функции , а именно: 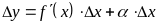. (8.1.1)

Определение 8.3. Дифференциалом функции 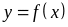в точке называется главная линейная частью её приращения, равная произведению производной 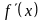в этой точке на произвольное приращение аргумента 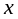, и обозначается (или ):

(8.4)

Дифференциал функции называют также дифференциалом первого порядка.

Под дифференциалом независимой переменной 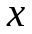понимается любое, независящее от , число. Чаще всего, в качестве этого числа берётся приращение переменной , т.е. . Это согласуется с правилом(8.4) нахождения дифференциала функции

Рассмотрим функцию и найдем её дифференциал.

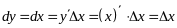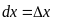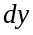, т.к. производная . Таким образом, получили: и дифференциал функции можно находить по формуле

. (8.4.1)

_{Замечание 8.7.} Из формулу (8.4.1) следует, что.

Таким образом, запись 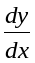можно понимать не только как обозначение для производной , но и как отношение дифференциалов зависимого и независимого переменных.

8.7. Геометрический смысл дифференциала функции

Пусть к графику функции проведена (см. рис. 8.1) касательная . Точка находится на графике функции и имеет абсциссу – . Даем произвольное приращение , такое, чтобы точка не вышла из области определения функции .

Рисунок 8.1 Изображение графика функции

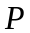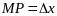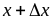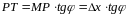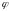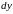Точка имеет координаты . Отрезок . Точка лежит на касательной к графику функции и имеет абсциссу – . Из прямоугольного следует, что , где угол – угол между положительным направлением оси и касательной, проведенной к графику функции в точке . По определению дифференциала функции и геометрического смысла производной функции в точке , делаем вывод, что 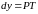. Таким образом, геометрический смысл дифференциала функции заключается в том, что дифференциал 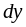представляет собой приращение ординаты касательной к графику функции 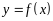в точке .

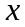Замечание 8.8. Дифференциал 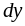и приращение для произвольной функции , вообще говоря, не равны между собой. В общем случае, разность между приращением и дифференциалом функции является бесконечно малой высшего порядка малости, чем приращение аргумента. Из определения 8.1 следует, что 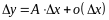, т.е. .

На рисунке 8.1 точка лежит на графике функции и имеет координаты . Отрезок .

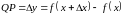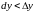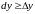На рисунке 8.1 выполнено неравенство , т.е. . Но возможны случаи, когда справедливо противоположное неравенство . Это выполняется для линейной функции и для выпуклой вверх функции.