Лекция 8

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ.

ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ ФУНКЦИЙ

8.1. Дифференцируемость функции в точке

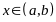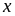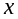Определение 8.1. Функции , определенная при всех , называется дифференцируемой в точке , если приращение этой функции в точке , соответствующее приращению аргумента 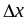, может быть представлено в виде

, (8.1)

где – некоторое число, не зависящее от , а 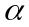– функция аргумента , которая является бесконечно малой при .

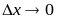Известно, что произведение двух бесконечно малых функций является бесконечно малой функцией более высокого порядка, т.е. 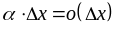. Тогда равенство (8.1) можно переписать в виде .

8.2. Необходимые и достаточные условия дифференцируемости функции в точке

Теорема 8.1. Для того чтобы функция 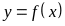была дифференцируема в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема в точке , тогда ее приращение представимо в виде (8.1). Рассмотрим отношение .

Из этого равенства следует, что существует предел левой части. Следовательно, существует производная .

Достаточность. Пусть функция имеет в точке конечную производную, т.е. существует предел . По теореме о связи функции, имеющей предел, и бесконечно малой функции можно записать

, где при 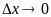. Умножая на обе части последнего равенства, получаем .

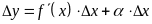Если обозначить 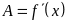– число, которое не зависит от , то получим формулу (8.1), что соответствует определению дифференцируемости функция в точке . Теорема доказана.

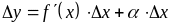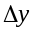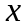Замечание 8.1. В теореме 8.1 получена формула , выражающая приращение функции в точке , соответствующее приращению аргумента , через значение производной 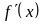этой функции. Тогда формула (8.1) при 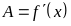примет следующий вид:

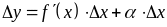(8.1.1)

Теорема 8.1 позволяет отождествлять понятия дифференцируемости функция в точке с понятием и существования у функции производной в точке .

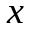Замечание 8.2. В лекции 7 в примере 7.1 рассмотрена непрерывная в каждой точке функция

Было показано, при эта функция не имеет производной, т.к. она имеет левую производную и правую производную . Следовательно, данная функция не дифференцируема при .

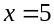8.3. Связь между непрерывностью и дифференцируемостью функции

Теорема 8.2. Если функция дифференцируема в точке , то она непрерывна в этой точке.

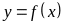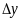Доказательство. Пусть функция дифференцируема в точке , тогда ее приращение представимо в виде (8.1). Найдем при предел . Получили: . Отсюда следует, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. А это означает непрерывность функции в данной точке .

Замечание 8.3. Из непрерывности функции 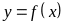в точке ещё не следует дифференцируемость функции в этой точке. Это иллюстрирует пример, приведённый в замечании 8.1.

Замечание 8.4. В точке разрыва функция не имеет производной.

Замечание 8.5. Производная непрерывной функции не обязательно будет непрерывной.

Определение 8.2. Функция 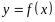называется гладкой на некотором множестве X, если она имеет непрерывную производную на этом множестве.

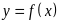Если производная допускает конечное число точек разрыва (причем первого рода), то функция называется кусочно-гладкой.