Лекция 2
Натуральные, целые, рациональные, иррациональные, действительные и комплексные числа, действия над ними.
Понятие переменной величины и функции
2.1. Натуральные, целые, рациональные, иррациональные, действительные числа, действия над ними
Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми.
Число является одним из первичных и основных понятий математики. Первоначально понятие отвлеченного числа отсутствовало, т.к. число было как бы «привязано» к тем предметам, которые пересчитывали. Древнегреческий математик Евклид считал, что число есть множество единиц. Отвлеченное понятие числа появилось вместе с развитием письменности.
Натуральными называются числа, которые используются для счёта предметов или обозначения номера предмета в ряду однородных предметов: 1, 2, 3, 4, 5, … . При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел не всегда могут не быть натуральными числами.
При дополнении натуральных чисел нулем и отрицательными числами
( т. е. числами, противоположными натуральным числам) получается множество целых чисел: ..., -3, -2, -1, 0, 1, 2, 3, … . При сложении, вычитании и умножении целых чисел всегда получается целые числа. Однако при делении целых чисел частное может и не быть целым числом.
Введение рациональных чисел, т. е. чисел
вида
, где
- целое число, а
- натуральное число, позволило
находить частное двух рациональных
чисел при условии, что делитель не равен
нулю. Каждое целое число m также является
рациональным, так как его можно
представить в виде
.
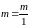При выполнении четырех арифметических
действии (кроме деления на нуль ) над
рациональными числами всегда получаются
рациональные числа. Рациональное число
можно представить в виде конечной или
бесконечной десятичной дроби. Однако,
операция извлечения корней из
положительного рационального числа,
может вывести из множества рациональных
чисел. Например,
– не являются рациональными числами.
Поэтому множество рациональных чисел
было дополнено множеством иррациональных
чисел.
Любое иррациональное число можно записать в виде бесконечной непериодической дроби, и любая непериодическая дробь является иррациональным числом. Иррациональные числа могут быть положительными и отрицательными, смотря по тому, измеряют ли они величины, считаемые положительными, или величины, считаемые отрицательными. Иррациональное число считается известным (или заданным), если указан способ, посредством которого можно находить любое число его десятичных знаков. Например,
=1,4142135…,
=
2,2360679… , число
—
математическая константа,
выражающая отношение длины окружности
к длине её диаметра;
=3,1415926…,
число
— математическая константа:
основание натуральных логарифмов,
названное в честь Эйлера; это так как
называемое число
Эйлера или число
Непера (Неперово число);
=2,
7182818… .
Множества рациональных и иррациональных чисел вместе составляют множество действительных чисел. Действительное число или как его еще называют вещественное число – это любое положительное число, отрицательное число или нуль.
Каждому действительному числу отвечает точка на координатной прямой, и наоборот, каждая точка на координатной прямой соответствует действительному числу. Действительно, для любой точки координатной прямой достаточно найти расстояние до неё от начала координат, а потом поставить перед этим числом знак плюс (+), если точка располагается правее начала координат, и знак минус (–) – если левее. Говорят, что каждая точка координатной прямой имеет действительную координату. Или иначе, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное соответствие. Координатная прямая является геометрической моделью множества действительных чисел; по этой причине для координатной прямой часто используют термин «числовая прямая».
Таблица 2.1.