
FTF 5 semestr.PROHOROV / Лекции / лекции_1-ядро
.pdf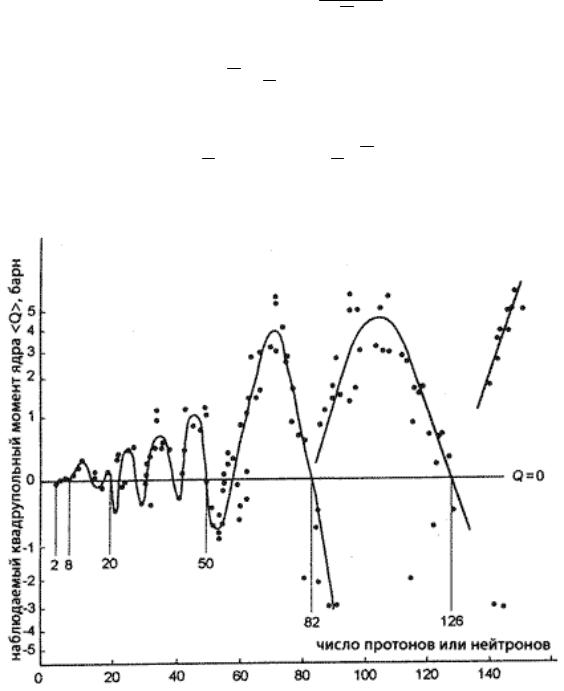
|
|
|
b a |
|
1 |
|
1 |
|
|
||
|
|
(b a) |
2 |
||
|
|
2 |
|||
|
|
|
|
|
|
R 1(b
b2 a2
R2
;
a),
2
то можно получить величину квадрупольного момента ядра
Q 2Z(b2 a2) 4ZR2 . 3 5
Обычно для ядер β < 0.6.
Рис. 7. Наблюдаемые квадрупольные моменты ядер Q
21

Рис. 8. Форма ядра 186Pb в различных состояниях
7. Ядерные силы. Модели ядра
Наблюдаемая на опыте устойчивость ядер означает, что ядерное взаимодействие не может быть сведено к электрическому, магнитному или гравитационному взаимодействиям. В самом деле, между протонами в ядре должна действовать кулоновская сила отталкивания. Наличие магнитных моментов у протонов может вызывать как притяжение, так и отталкивание (в зависимости от взаимной ориентации магнитных моментов). Гравитационная сила, хотя и отвечает притяжению нуклонов, намного слабее кулоновской. Следовательно, в случае атомных ядер имеет место особое взаимодействие. Это взаимодействие называют сильным, а отвечающие ему силы – ядерными. Ядерные силы – это силы, действующие между нуклонами и удерживающие их в ядре.
Основные свойства ядерных сил:
1)являются силами притяжения;
2)являются короткодействующими: действие ядерных сил прояв-
ляется только тогда, когда расстояние между двумя нуклонами ~ 10–15 м; с увеличением расстояния они быстро уменьшаются до нуля, а при расстояниях, меньших их радиуса действия, примерно в 100 раз больше кулоновских сил, действующих между протонами (на том же расстоянии);
3)обладают зарядовой независимостью: ядерные силы двух нукло-
нов не зависят от их электрических зарядов. Силы, действующие между двумя протонами, или двумя нейтронами, или между протоном и нейтроном, за вычетом кулоновских сил одинаковы. Это указывает на неэлектри-
ческую природу ядерных сил;
22
4)имеют способность к насыщению: каждый нуклон в ядре взаимо-
действует только с ограниченным числом ближайших к нему нуклонов. Это свойство проявляется в том, что удельная энергия связи нуклонов в ядре (за исключением легких ядер) с увеличением числа нуклонов не растет, оставаясь приблизительно постоянной;
5)зависят от взаимной ориентации спинов взаимодействующих
нуклонов: протон и нейтрон, например, образуют дейтрон (21H) только при параллельной ориентации их спинов;
6) не являются центральными силами: их нельзя представить в ви-
де сил, действующих от одного центра сил. Это обусловлено наличием спина взаимодействующих частиц.
Создание единой последовательной теории атомного ядра до настоящего времени затруднено из-за сложного характера и недостаточной определенности данных о ядерных силах, из-за громоздкости и трудности точного решения квантовых уравнений, описывающих движение большого числа нуклонов в ядре, из-за обязательности учета движения нуклонов вследствие сильного взаимодействия между ними. Поэтому в теории ядра используют модельный подход, основанный на аналогии свойств атомных ядер со свойствами, например, жидкой капли, электронной оболочки атома и т.д.: соответственно модели ядер называют капельной, оболочечной и т.д. Каждая из моделей описывает только определенную совокупность свойств ядра, а потому, обладая ограниченными возможностями, не может дать его полного описания.
8. Модель жидкой капли
Капельная модель (Н.Бор, Я.И.Френкель, 1936) – простейшая и исторически первая модель ядра; она базируется на аналогии в поведении нуклонов в ядре и молекул в капле жидкости. Так, в обоих случаях силы, действующие между составными частицами – молекулами в жидкости и нуклонами в ядре, – являются короткодействующими и им свойственно насыщение. Кроме того, для капли жидкости характерна постоянная плотность вещества, не зависящая от числа молекул, входящих в каплю. Ядра также характеризуются примерно одинаковой плотностью ядерного вещества, не зависящей от числа нуклонов в ядре. В капле жидкости и атомном ядре наблюдается определенная подвижность составных частиц. Наконец, объем капли, так же как и объем ядра [см. (1)], пропорционален числу частиц. Подобное сходство свойств позволило трактовать в капельной модели ядро как каплю электрически заряженной несжимаемой жидкости (с плотностью, равной ядерной), подчиняющуюся законам квантовой механики.
Итак, свойство насыщения ядерных сил, вытекающее в свою очередь
23
из их короткодействия и отталкивания на малых расстояниях, делает ядро похожим на жидкость. Силы, связывающие молекулы жидкости, тоже насыщаются, а энергия испарения линейно увеличивается с увеличением массы. На этой основе был создан способ описания ядра в модели жидкой капли (Вайцзеккер, 1935 г.).
Зачем вообще нужны модели ядра, заранее навязывающие ему определенные свойства? Можно ли решить задачу без моделей, строго?
Ядро – совокупность нуклонов, каждый из которых сохраняет свою структуру и свойства. Действительно, масса нуклона 940 МэВ/с2, а для перевода нуклона в первое возбужденное состояние нужна энергия300 МэВ. В то же время средняя кинетическая энергия нуклона в ядре
<TN> 20 МэВ.
Так же как в кинетической теории газов можно не учитывать атомную структуру, а при описании атома – ядерную, при описании ядра можно не учитывать структуру нуклонов. Кроме того, поскольку
<TN> 20 МэВ << mNc2 940 МэВ,
то правомерно использование нерелятивистской квантовой теории, т.е. уравнения Шредингера для системы A частиц. Гамильтониан ядра H может быть записан в виде
|
A |
|
1 |
A |
A |
|
|
H T |
U , |
||||||
2 |
|||||||
|
1 |
|
|
1 |
1 |
|
|
где T p2 /2m – оператор кинетической энергии нуклона, U – потен-
циал взаимодействия нуклонов и (парный потенциал) и вышеприведенные два варианта записи энергии взаимодействия исключают учет энергии взаимодействия одной и той же пары нуклонов дважды. Величина U
близка к потенциалу элементарного нуклон-нуклонного (NN) взаимодействия. Последнее уточняется в физике высоких энергий (физике частиц), а на долю теории ядра остается решение задачи многих тел.
Трудности решения уравнения H E для ядра:
1.NN-взаимодействие до конца не изучено.
2.Проблема A сильно взаимодействующих тел строго не решена для A > 4 (это главная трудность).
Эту последнюю трудность можно обойти, используя для упрощения модели ядра, в которых уже задаются (угадываются) некоторые наиболее существенные его свойства. Одна из первых и простейших моделей ядра – модель жидкой капли, откуда следует формула Вайцзеккера для энергий связи ядер в основном состоянии. Сходство жидкой капли и ядра основано
24

на следующих двух пунктах:
1.В обоих случаях энергия связи пропорциональна числу составляющих частиц.
2.Радиальная форма NN-потенциала (рис. 9) аналогична (если не учитывать разницу в масштабах) потенциалу Леннард-Джонса для двух молекул.
В этой модели можно получить полуэмпирическую формулу (фор-
мула Вайцзеккера), определяющую энергию связи ядра и выраженную через его массовое A и зарядовое Z числа:
Eсв(A, Z) A A2/3 Z2 / A1/3 (A 2Z)2 / A A 3/4, (39)
где коэффициенты 14.0; 13.0; 0.584; 19.3, причем = 0 для ядер с нечетным значением А, а можно выразить через радиус ядра R:
Z2 / A1/3 3(Ze)2 /5R.
Рис. 9. Распределение NN-потенциала U
В общем случае коэффициент определяется следующим образом:
1, |
при четных A и Z, |
|
|
0, |
при нечетном A (Z любое), |
33,5 |
||
|
1, |
при четном A и нечетном Z. |
|
||
В формулу энергии связи для ядра входит ряд членов, каждый из которых отвечает за конкретный составляющий вид энергии.
Объемная энергия. Энергия связи ядра тем больше, чем больше в нем нуклонов или объем ядра. Поскольку этот объем пропорционален A, то энергию ядра в первом приближении можно записать в виде так называемой «объемной» энергии:
Eоб = + A,
25

где – константа ( > 0).
Если этим ограничиться, то мы имеем дело с бесконечной ядерной материей (поверхностные эффекты не существенны), лишенной заряда (пренебрегаем кулоновским отталкиванием).
Поверхностная энергия. Нуклоны на поверхности связаны менее сильно, чем внутри, т.к. взаимодействуют с меньшим числом своих партнеров, чем внутренние нуклоны. Если в бесконечной ядерной материи провести поверхность, ограничивающую ядро, и отбросить нуклоны вне ее, то оставшиеся у поверхности нуклоны ядра потеряют половину своих связей.
Число потерянных связей пропорционально числу нуклонов на по-
верхности, а следовательно и площади поверхности, которая равна S = 4 R2 = 4 r0 A2/3, где R = r0 A1/3 – радиус ядра. Итак, за счет поверхности,
энергия связи уменьшается на величину A2/3, т.е. в формулу для энергии связи необходимо добавить (со знаком «минус») слагаемое, которое будем называть поверхностной энергией
Eпов = A2/3,
где – константа ( > 0).
На нуклон, находящийся на поверхности, действует результирующая сила, направленная внутрь ядра. Поэтому поверхностные нуклоны стремятся сжать ядра, создавая, как и в капле жидкости, поверхностное натяжение, энергия которого и определяется выражением для Eпов.
Кулоновская энергия. Эту энергию легко оценить для заряда, равномерно распределенного по объему сферы с плотностью = Ze/(4/3) R3. Тогда энергия кулоновского отталкивания Z протонов ядра (в предположении равномерного распределения заряда +Ze внутри сферы радиусом R), уменьшающая энергию связи, дается классической электростатической энергией такого распределения
Eкул |
3 |
(Ze)2 |
|
Z2 |
||
|
|
|
|
|
, |
|
5 |
|
R |
A1/3 |
|||
откуда по известному R = r0 A1/3 находят коэффициент :
3e2 .
5 r0
Ограничиваясь членами Eоб, Eпов и Eкул, нельзя получить правильный ход линии стабильности. Для легких ядер эта линия отвечает приблизительному равенству чисел протонов и нейтронов (N Z). В то же время, из выше рассмотренных трех членов для энергии связи, при фиксированном A от Z зависит лишь кулоновский. Ввиду этого максимум энергии связи достигается при Z = 0 и стабильные ядра должны были бы состоять из одних
26

нейтронов. Очевидно это не так и связано это с тем, что не учтена кванто-
вая природа ядерной капли.
Энергия симметрии. Чтобы получить правильный ход линии стабильности, необходимо учесть принцип Паули (ядро состоит из фермионов, подчиняющихся этому принципу). Вследствие этого ядра, у которых нуклонов одного типа больше, чем другого, имеют меньшую энергию связи, чем ядра с одинаковым числом протонов и нейтронов. Это хорошо видно из рис. 10, где показано расположение 4-х нуклонов по уровням энергий в прямоугольной потенциальной яме в некоторой условной модели (наподобие модели Ферми-газа) для двух случаев:
а) 2 протона + 2 нейтрона (без учета кулоновской энергии); б) 4 нейтрона.
Предполагаем, что каждый уровень характеризуется лишь одним набором квантовых чисел и поэтому в соответствии с принципом Паули может быть занят лишь одним нуклоном каждого типа.
Считая, что уровни эквидистантны и расстояние между ними (а также глубина наиболее мелко сидящего уровня) равны E, получаем для левого варианта (а), энергию связи (т.е. энергию, необходимую для того, чтобы «достать» все нуклоны из потенциальной ямы) Ea = 14 E, а для правого (б)
– Eб = 10 E, т.е. Ea > Eб. Если даже создать ядро из одних нейтронов или протонов, то оно путем процессов n p (или p n) перейдет в ядро с приблизительно равным числом нейтронов и протонов (эти процессы – не что иное как -распад.
Рис. 10. Расположение нуклонов по уровням энергий в прямоугольной потенциальной яме
Член в формуле Вайцзеккера, который учитывает стремление ядра иметь в основном состоянии симметричное расположение по уровням нейтронов и протонов (симметрийный член), может быть записан в следующем виде:
27
Eсим |
(N Z)2 |
(A 2Z)2 |
||
|
|
|
. |
|
|
|
|||
|
A |
A |
||
Квадратная степень в числителе отражает тот факт, что энергия симметрии должна возрастать при росте относительного числа нуклонов любого типа. Появление множителя A–1 связано с реальным сближением ядерных уровней с ростом A. Слагаемое Eсим должно быть добавлено в формулу Вайцзеккера со знаком «минус» потому, что отклонение от симметрии уменьшает энергию связи.
Равновесное число протонов Zравн (линия стабильности) в ядре при фиксированном A определяется минимумом по Z суммы 3-го и 4-го членов в формуле Вайцзеккера (39), откуда легко получить
Zравн |
2 A |
|
A |
||
|
|
|
|
. |
|
A2/3 4 |
0,015A2/3 1,98 |
||||
Видно, что Zравн < A/2. При |
|
отсутствии кулоновской энергии |
|||
Zравн = A/2. При учете кулоновской энергии линия стабильности с ростом Z все более смещается в сторону большего числа нейтронов.
Эффект спаривания. С помощью полученной четырехчленной формулы Вайцзеккера можно описать энергию связи ядер (исключая легкие с A 20) с точностью 1 %. Однако имеются «пульсации» на уровне 1–2 МэВ, которые объясняются специфическим свойством NN-взаимодействия
– в основном состоянии ядра возникает дополнительная связь между двумя нуклонами одного типа (двумя протонами или двумя нейтронами), занимающими один и тот же энергетический уровень. Этот эффект невелик ( 1–3 МэВ), т.е. всего 0,2 % от энергии связи ядра, но четко виден в зависимости энергии связи от A, Z и N. Он демонстрируется на рис. 11 для энергии отделения нейтрона изотопов Ce (церия).
Видно, что энергия отделения нейтрона возрастает на 2–3 МэВ, когда их число становится четным. Это объясняется обсуждаемым особым свой-
ством NN-взаимодействия: возникновением в основном состоянии ядра
дополнительной связи между двумя нуклонами одного типа, находящимися на одном и том же энергетическом уровне. Качественно этот эффект иллюстрируется рис. 12, где схематически показано, как меняется энергия отделения внешнего нейтрона при последовательном увеличении их числа.
С точки зрения обсуждаемого эффекта (или, как говорят, сил спаривания) все ядра разбиваются на три типа:
–четно-четные ядра (все нуклоны в основном состоянии спарены и положительная добавка к энергии связи наибольшая);
–нечетно-нечетные ядра (не спарены в основном состоянии по од-
28

ному нуклону каждого типа и добавка к энергии связи наименьшая);
– промежуточный случай – нечетные ядра (один нуклон в основном состоянии неспарен).
Рис. 11. Энергии отделения нейтрона изотопов церия
Рис. 12. Спаривание нуклонов в ядре. Энергия спаривания 1–3 МэВ.
Вверхней части рисунка показаны проекции моментов
успариваемых нуклонов
Спаривательное слагаемое Eсп в формуле для Eсв(A, Z) условились записывать так, чтобы для нечетных ядер оно было равным нулю. В этом случае наилучшее воспроизведение экспериментальных данных дает следующая формула:
Eсп = A–3/4,
29
где = +| | для четно-четных ядер; = 0 для нечетных ядер; = –| | для не- четно-нечетных ядер и | | = 33,5 МэВ.
Итак, окончательное выражение для энергии связи ядра (формула Вайцзеккера) имеет пятичленную структуру и принимает вид (39).
Приведем распределение числа стабильных ядер в зависимости от типа (четно-четные, нечетные, нечетно-нечетные).
Таблица 3
Z |
N |
A |
Число стабильных ядер |
|
|
|
|
ч (четное) |
ч |
ч |
165 |
н (нечетное) |
ч |
н |
53 |
ч (четное) |
н |
н |
57 |
н (нечетное) |
н |
ч |
8 |
|
|
|
всего: 283 |
Стабильные нечетно-нечетные ядра: 21H, 63Li, 105B, 147 N.
Долгоживущие нечетно-нечетные ядра с измеренным процентным содержанием в естественной смеси изотопов: 4019K, 5023V, 13857La, 17671Lu.
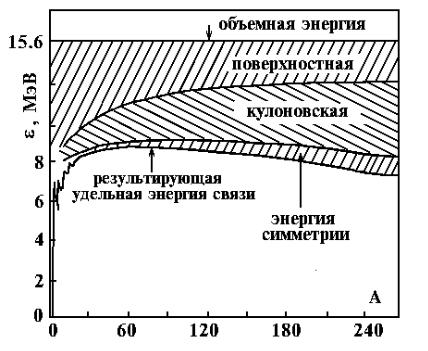
Вклад различных членов в формулу для удельной энергии связи иллюстрируется рис. 13.
Рис. 13. Вклад различных членов в формулу для удельной энергии связи
В заключение приведем таблицу синтезированных сверхтяжелых элементов с Z 100:
30
